Предмет: Математика,
автор: kusorest
Помогите, пожалуйста, решить комбинированный №15 из ЕГЭ по математике (бывш. С3)
Ответ 
Приложения:
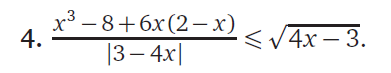
Ответы
Автор ответа:
0
*Не думаю что это решение лучшее, но другого я просто не увидел.
Найдем ОДЗ:


Исходя из данных ограничений, можно открыть модуль и переписать неравенство в другом виде:

Числитель дроби можно преобразовать:

Таким образом мы пришли к этому:

Перенесем все в одну часть, внесем под один знаменатель:

Раскроем числитель как разность кубов:

Попробуем решить это неравенство методом интервалов, т.е. для начала найдем нули функции:
1)

Единственное решение
(и второе решение не влияет на знак неравенства, положительно)
2)

После частичного упрощения верхнего уравнения системы получим:

Дальше решать смысла нет, т.к. верхнее уравнение не будет иметь решений (левая часть равенства всегда отрицательна, правая - положительна)
Одновременно с этим знак выражения

на допустимом (ОДЗ) интервале всегда положителен, поэтому оно никак не влияет на знак неравенства.*
Тогда все наше первоначальное неравенство эквивалентно данному:

Его решением и будет являться (с учетом ОДЗ)

* Можно обосновать так:
 (в нашем случае уместно)
(в нашем случае уместно)
 , коэффициент при числе в квадрате положителен, значит и все значения функции на интервале ОДЗ положительны.
, коэффициент при числе в квадрате положителен, значит и все значения функции на интервале ОДЗ положительны.
Найдем ОДЗ:
Исходя из данных ограничений, можно открыть модуль и переписать неравенство в другом виде:
Числитель дроби можно преобразовать:
Таким образом мы пришли к этому:
Перенесем все в одну часть, внесем под один знаменатель:
Раскроем числитель как разность кубов:
Попробуем решить это неравенство методом интервалов, т.е. для начала найдем нули функции:
1)
Единственное решение
(и второе решение не влияет на знак неравенства, положительно)
2)
После частичного упрощения верхнего уравнения системы получим:
Дальше решать смысла нет, т.к. верхнее уравнение не будет иметь решений (левая часть равенства всегда отрицательна, правая - положительна)
Одновременно с этим знак выражения
на допустимом (ОДЗ) интервале всегда положителен, поэтому оно никак не влияет на знак неравенства.*
Тогда все наше первоначальное неравенство эквивалентно данному:
Его решением и будет являться (с учетом ОДЗ)
* Можно обосновать так:
Похожие вопросы
Предмет: Английский язык,
автор: alisha22889
Предмет: Қазақ тiлi,
автор: markasem
Предмет: История,
автор: mergenbaevaaminatd
Предмет: Физика,
автор: homikadze
Предмет: Химия,
автор: Konfetkafack