Question

в прямоугольном треугольнике а и в-длины катетов, с-длина гипотенузы. докажите, что радиус окружности, касающейся гипотенузы и продолжения катетов этого треугольника равен (а+в-с)/2

Answer 1

Помощь в решение,использовал:

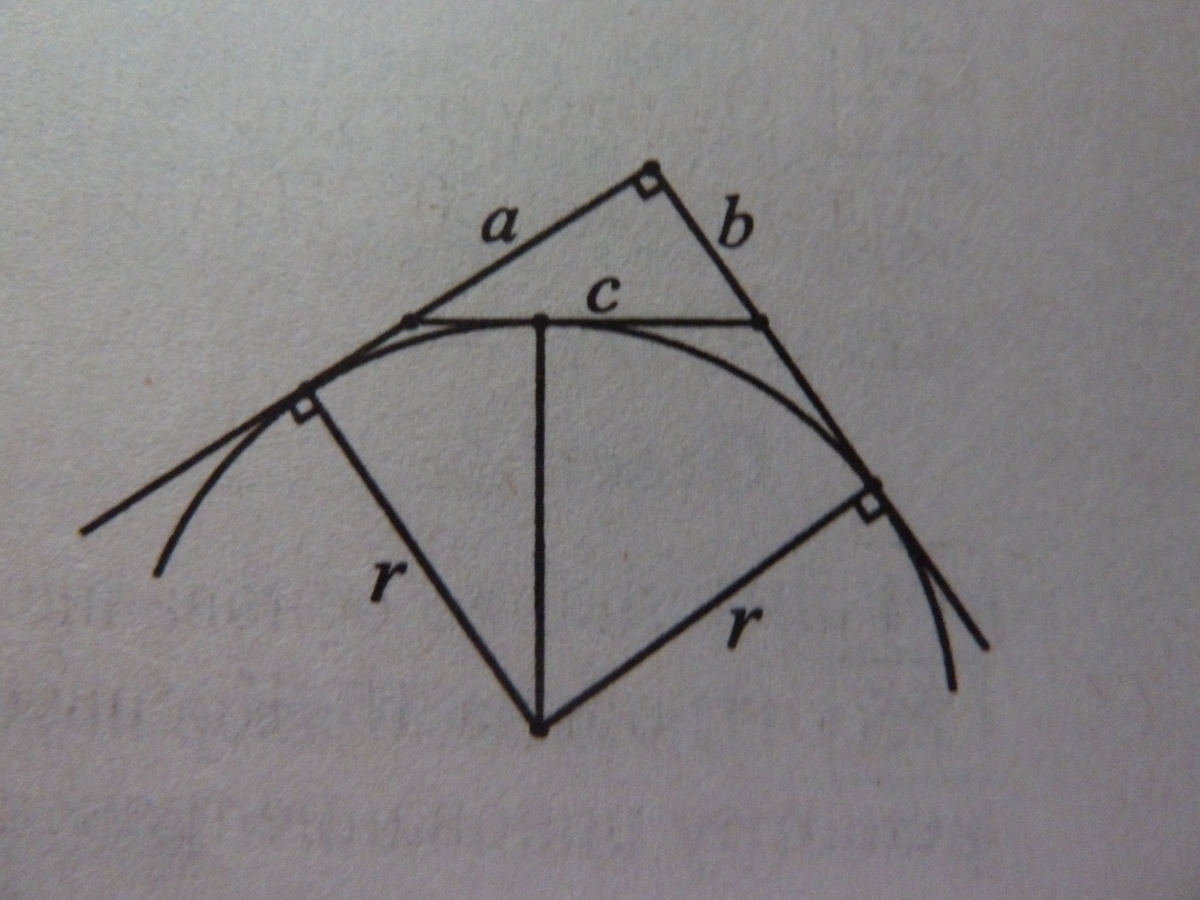
Четырёхугольник, образованный прямыми, содержащими катеты, и радиусами, проведёнными в точки касания с продолжениями катетов, -- квадрат.

Решение:

Обозначим вершины треугольника, противолежащие сторонам a, b, c, через A, B, C (C — вершина прямого угла), а точки касания — через A1, B1, C1 соответственно. Если O — центр данной окружности, то OA1CB1 — квадрат со стороной, равной r. Поэтому

CA1 = r, BC1 = BA1 = r - a, AC1 = AB1 = r - b,

c = AB = AC1 + C1B = 2r - a - b.

Следовательно, r =a+b+c/2.

Если помог поставьте лучшее решение.Спасибо.