Помогите пожалуйста с "практикумом наглядная геометрия 7 класс"
Ответы
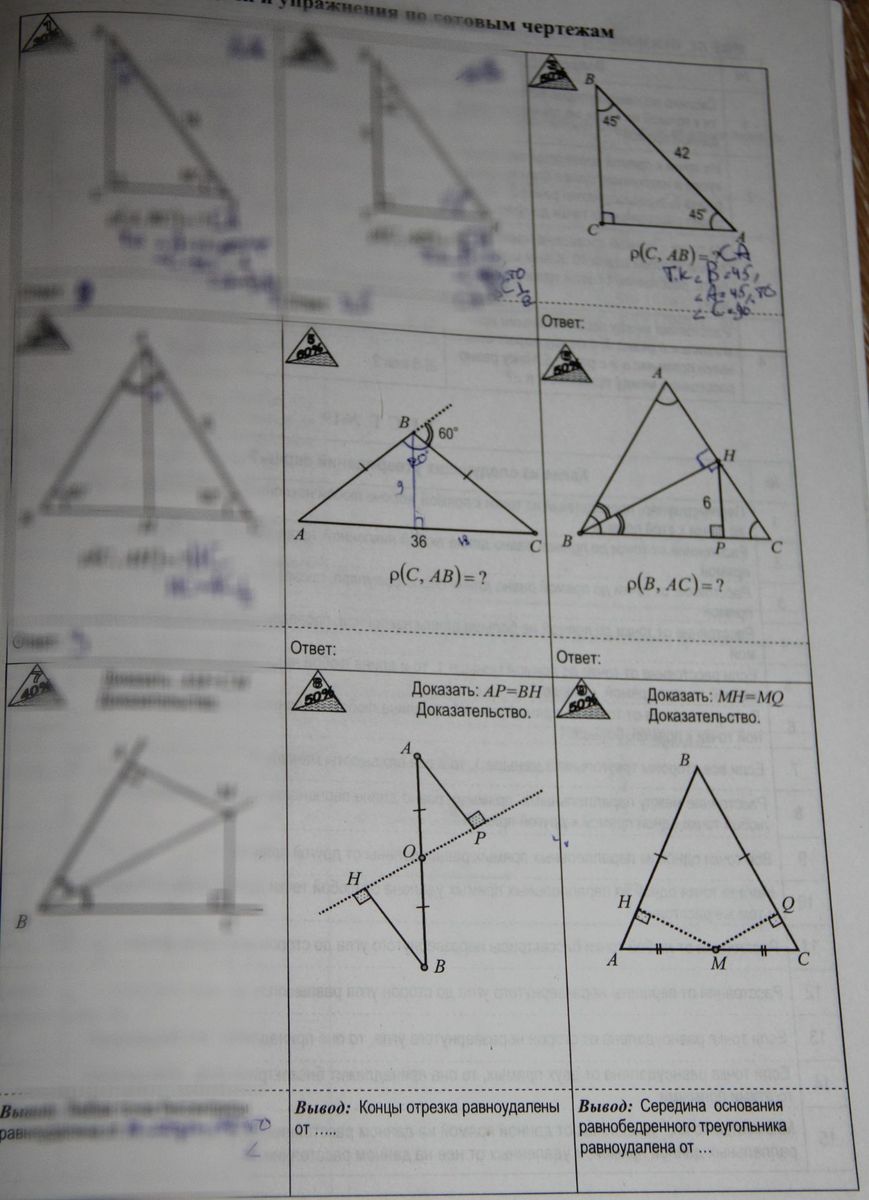
Задача №3
АВ уже дано в задаче, скорее всего следует найти АС и ВС
Дан треугольник с равными углами при стороне АВ . Углы равны 45 градусам, отсюда угол С=180-2*45=90 , а треугольник АВС - равнобедернный.
АВ - гипотенуза этого треугольника и ее квадрат равен сумме квадратов катетов ВС и АС, а так как ВС=АС, то
АВ²=2АС²
АС²= АВ²:2=16:2=882
АС=21√2
--------------------
Задача №5
Дан равнобедренный треугольник. Внешний угол при вершине В равен 60 градусов. Так как внешний угол треугольника равен сумме двух внутренних, не смежных с ним, то сумма углов А+С =60, а каждый из них равен 30 градусам.
АВ - гипотенуза прямоугольного треугольника, в котором сторона против угла А равна половине этой гипотенузы. (В треугольнике АВС это его высота, медиана и биссектриса - "три в одном флаконе")..
Пусть эта эта сторона равна х, тогда АВ=2х По теореме Пифагора
4х²=(36:2)²+х²
3х²=324
х²=108
х=6√3
АВ=2*6√3=12√3
------------------------
Задача №6
Треугольник АВС - равносторонний, т.к. углы А, В и С в нем равны по условию ( см. рисунок) . АС=АВ=ВС.
ВН - биссектриса, высота и медиана треугольника АВС.
АС=2 НС или АН+НС, т.к. эти отрезки равны ( вспомним, что ВН- медиана.)
Все углы треугольника АВС равны 180:3=60 градусов.
Углы, на которые биссектрсса делит угол В, равны 30 градусов.
НР противолежит углу 30 градусов.
Отсюда ВН=2НР=12
АН противолежит углу 30 градусов. АВ=АС=2 АН
АВ²=ВН²+АН²
4АН²=144+АН²
3АН²=144
АН²=48
АН=4√3
АС=АВ=8√3
-----------------------------------
Задача №8
Треугольники АРО и ВНО равны. Это прямоугольные треугольники ( углы Н и Р - прямые по рисунку), углы при О в них равны, гипотенузы АО=ОВ.
Если в прямоугольном треугольнике острый угол и гипотенуза равны острому углу и гипотенузе другого прямоугольного треугольника, эти треугольники равны.
Следовательно, АР=ВН
Вывод: Концы отрезка АВ равноудалены от прямой НР
-------------------------
Задача №9
Дан равнобедренный треугольник АВС. АВ=ВС
АМ=МС.
МН и МQ- перпендикуляры к боковым сторонам треугольника.
Так как треугольник равнобедренный, углы А и С в прямоугольных треугольниках
АНМ и МQC равны.
Гипотенузы АМ=МС .
Если в прямоугольном треугольнике острый угол и гипотенуза равны острому углу и гипотенузе другого прямоугольного треугольника, эти треугольники равны.
Кратчайшее расстояние от точки до прямой - перпендикуляр.
Перпендикуляры к боковым сторонам в равных треугольниках АНМ и МQC равны.
НМ=QМ
Вывод: середина основания равнобедренного треугольника АВс равноудалена от его боковых сторон.