Предмет: Алгебра,
автор: pivabaleechingnet
Можете пожалуйста решить примеры. 5, 6, 7, 8 - нужно найти дифференциалы первого порядка. а номера 1, 2, 3, 4, 5 - найти дифференциалы второго порядка. Прошу сколько сможете. Спасибо!
Приложения:
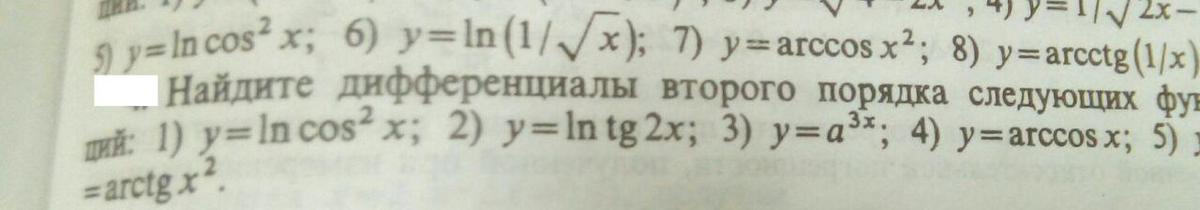
Ответы
Автор ответа:
0
Автор ответа:
0
почемк в. таком виде?
Автор ответа:
0
Перезагрузи страницу, будут формулу (не с телефона). Это на сайте глючит редактор формул.
Автор ответа:
0
ok, дома зайду, сейчас нет возможности
Похожие вопросы
Предмет: Математика,
автор: glagolievmaxim
Предмет: Физика,
автор: asal00
Предмет: Геометрия,
автор: 3345565554332
Предмет: География,
автор: irinaelena26
Предмет: Алгебра,
автор: L000oooooooooooooooL