Предмет: Геометрия,
автор: 3345565554332
 Все плоские углы при вершине треугольной пирамиды равны 30 градусов. Определите двугранные углы при ее блоковых рёбрах. Ответ должен быть arccos (2 корень из 3-3)
Ответы
Автор ответа:
2
Если угол при вершине боковых граней равен 30 градусов, то углы при основании их равны по 75 градусов.
Примем сторону основания за 1.
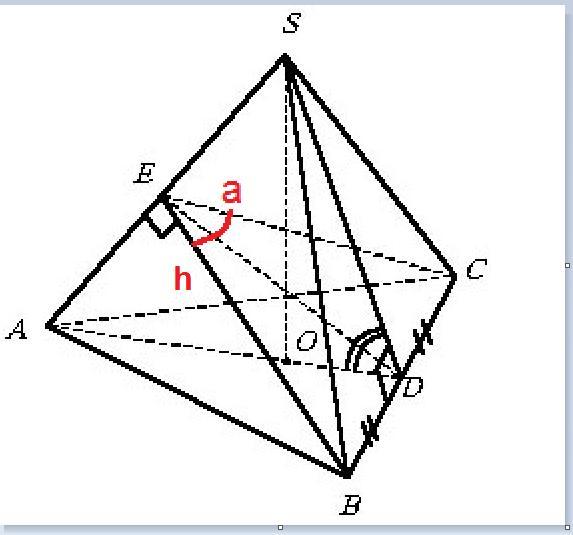
Тогда высота на боковое ребро h равна 1*cos(30°/2).
В этой задаче надо определить косинус половинного угла.
Для косинуса 15 градусов есть несколько вариантов.
Можно так: cos 15° = cos(60° - 45°).
Подставив данные, получим cos 15° = (√2 + √6)/4.
Можно так: cos 15° = √(1 + cos30°)/2 = √(1 + (√3/2))/2.
Подставив данные, получим cos 15° = (√(2 + √3))/2.
Можно и в таком варианте: cos 15° = (√3 + 1)/(2√2 ).
Угол между боковыми гранями равен плоскому углу между высотами к боковому ребру.
По формуле косинусов этот угол равен:
α = arc cos((h² - 1)/(2h²)).
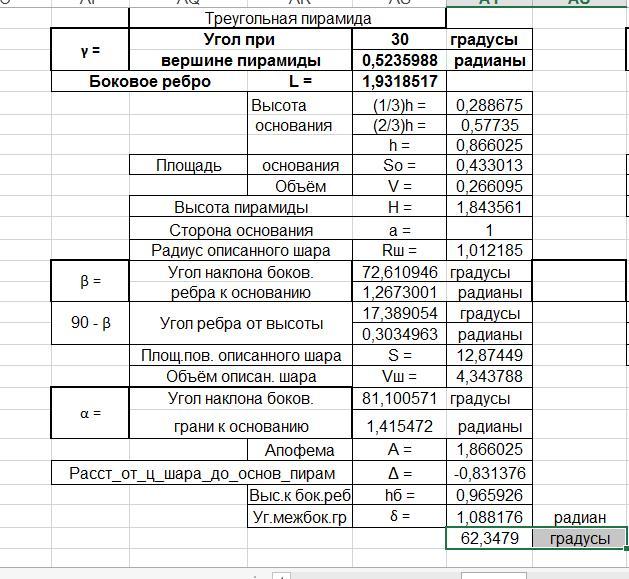
Подставив данные, получаем α = 62,34790439 градусов.
Приложения:
ata221:
https://znanija.com/task/43198925 помогите, пожалуйста
Похожие вопросы
Предмет: Українська мова,
автор: Vitysichka03097
Предмет: Русский язык,
автор: VinokurovaVika3591
Предмет: Другие предметы,
автор: мишакласс
Предмет: Алгебра,
автор: zizi21878
Предмет: Немецкий язык,
автор: NEoning