Предмет: Алгебра,
автор: kukushkinao
Ребят помогите пожалуйста спасите от двойки((подробно
Приложения:

Ответы
Автор ответа:
0
_________________________
Приложения:
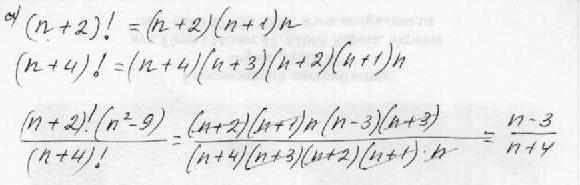
Автор ответа:
0
a)

б)

в)

г)

k²+5k+6=0
D=5²-4*6=25-24=1
k₁=(-5-1)/2=-3 k₂=(-5+1)/2=-2
k²+5k+6=(k+3)(k+2)


б)
в)
г)
k²+5k+6=0
D=5²-4*6=25-24=1
k₁=(-5-1)/2=-3 k₂=(-5+1)/2=-2
k²+5k+6=(k+3)(k+2)
Приложения:
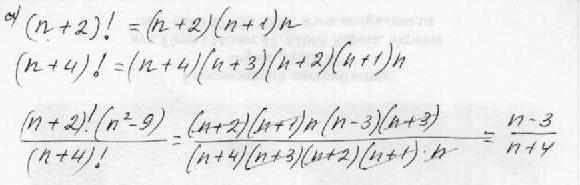
Похожие вопросы
Предмет: Литература,
автор: firdavshasanov318
Предмет: Окружающий мир,
автор: anastasia94466
Предмет: Алгебра,
автор: olekciu222
Предмет: Математика,
автор: wotrutest
Предмет: Геометрия,
автор: ipochtarev01