Предмет: Алгебра,
автор: lenok981
Помогите решить систему уравнений
Приложения:
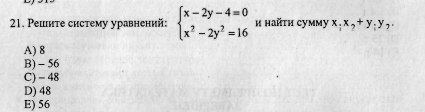
Ответы
Автор ответа:
1
x = 2y + 4;
(2y + 4)^2- 2y^2 - 16 = 0 *
* 4y^2 + 16y + 16 - 2y^2 - 16 = 0
2y^2 + 16y = 0
y^2 + 8y = 0
y (y + 8) = 0
y1 = 0
y2 = - 8
x1 = 2y1 + 4 = 2*0 + 4 = 4;
x2 = 2y2 + 4 = 2*(-8) + 4 = - 16 + 4 = - 12
Ответ:
x1 * x2 + y1*y2 = 4*(-12) - 8*0 = - 48
(2y + 4)^2- 2y^2 - 16 = 0 *
* 4y^2 + 16y + 16 - 2y^2 - 16 = 0
2y^2 + 16y = 0
y^2 + 8y = 0
y (y + 8) = 0
y1 = 0
y2 = - 8
x1 = 2y1 + 4 = 2*0 + 4 = 4;
x2 = 2y2 + 4 = 2*(-8) + 4 = - 16 + 4 = - 12
Ответ:
x1 * x2 + y1*y2 = 4*(-12) - 8*0 = - 48
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Геометрия,
автор: Andhak
Предмет: Английский язык,
автор: a4586745
Предмет: Математика,
автор: denchuk777
Предмет: Физика,
автор: LolisPopis