Question

Постройте график функции
y=$(x-2)^{2} -1$
Укажите для этой функции:
а) область определения;
б) нули;
в) промежутки знакопостоянства;
г) промежутки возрастания (убывания);
д) область изменения.

Answer 1

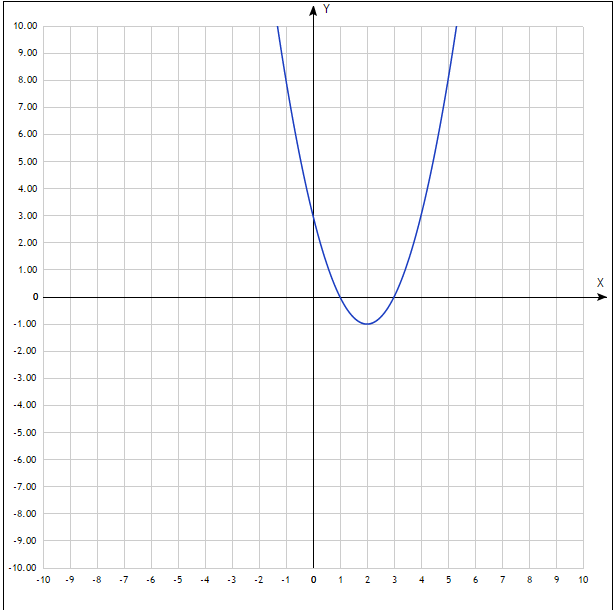
График будет во вложении.

а)
Так как это квадратичная функция, и ее график парабола. То как известно:
$D(f)=(-\infty,\infty)$

b)
$(x-2)^2-1=0$
$x^2-4x+4-1=0$
$x^2-4x+3=0$
$\sqrt{D}= \sqrt{16-12}=2$
$x_{1,2}= \frac{4\pm2}{2}=3,1$
Сразу для будущего я упрощу нашу функцию по теореме Виета:
$y=(x-3)(x-1)$
c)
Отметим эти 2 точки на числовой прямой , и получим 3 интервала и их знаки:
$(-\infty,1)=+$
$(1,3)=-$
$(3,+\infty)=+$

То есть, на 1 и 3 интервалах, функция положительна, на 2 интервале, отрицательна.
 Конечный ответ:
$y\ \textgreater \ 0$, если $x\in (-\infty,1) \cup (3,+\infty)$

И
$y\ \textless \ 0$, если $x\in (1,3)$

d)
Так как коэффициент а>0 то ветви параболы смотрят вверх, и вершина такой параболы является минимумом функции.
Найдем вершину:
$x= \frac{4}{2}=2$
$y=(2-3)(2-1)=-1$
$(2,-1)$
Все сделано по формулам вершины.
Так как вершина является минимумом. То производная данной функции меняет в этой точке свой знак с минуса на плюс. 
Отсюда следующие промежутки убывания и возрастания:
Функция убывает на интервале $(-\infty,2)$
Функция возрастает на интервале $(2,+\infty)$

e)
Область изменения = Область значений.
Аналитически это слишком долго находить, поэтому решим это смотря на график.
Мы видим что есть минимум, после минимума функция возрастает, и не идет больше вниз.
То есть:
$E(f)=[-1;+\infty)$