Предмет: Алгебра,
автор: kroditji
Привет,помоги пожалуйста с алгеброй
Докажите неравенство:
а) (x-4) (x+2)>(x-5) (x+3);
б) (m-4) (m+6)<(m+3) (m-1);
в)  +1
+1  2x.
2x.
Ответы
Автор ответа:
1
Вот решение и первого, и второго и третьего
Приложения:

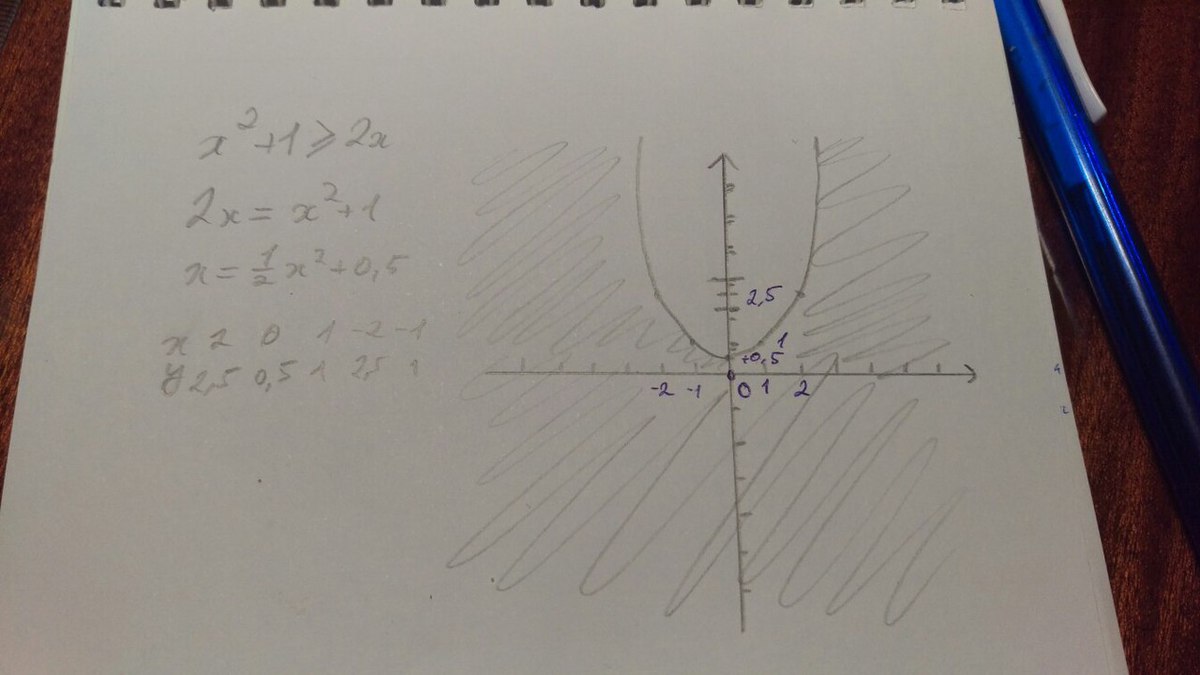
Автор ответа:
2
Докажите неравенство:
а) (x-4) (x+2)>(x-5) (x+3);
б) (m-4) (m+6)<(m+3) (m-1);
в) x² +1 ≥2x.
----
Определение :A>B, если A-B >0 ; A<B, если A-B <0 .
а) (x-4) (x+2)- (x-5) (x+3) =(x² +2x -4x -8) -(x²+3x-5x -15) =7 >0.
---
б) (m-4) (m+6)- (m+3) (m-1) =(m²+6m-4m-24) -(m²-m+3m-3) =-21<0 .
---
в) x² +1 -2x =(x-1)²≥0 . равенство при x =1.
а) (x-4) (x+2)>(x-5) (x+3);
б) (m-4) (m+6)<(m+3) (m-1);
в) x² +1 ≥2x.
----
Определение :A>B, если A-B >0 ; A<B, если A-B <0 .
а) (x-4) (x+2)- (x-5) (x+3) =(x² +2x -4x -8) -(x²+3x-5x -15) =7 >0.
---
б) (m-4) (m+6)- (m+3) (m-1) =(m²+6m-4m-24) -(m²-m+3m-3) =-21<0 .
---
в) x² +1 -2x =(x-1)²≥0 . равенство при x =1.
Похожие вопросы
Предмет: Химия,
автор: nazar33333
Предмет: Математика,
автор: ainurkenzhegulova8
Предмет: Английский язык,
автор: dzubenkohasta
Предмет: Алгебра,
автор: Arina12131415
Предмет: Математика,
автор: dashaudalova621