Предмет: Алгебра,
автор: AlexanderGoga
1.Производная
2. Найти тангенс угла наклона касательной к графику f(x) в точке х0Ю если...
23. Написать уравнение касательной к графику...
Приложения:
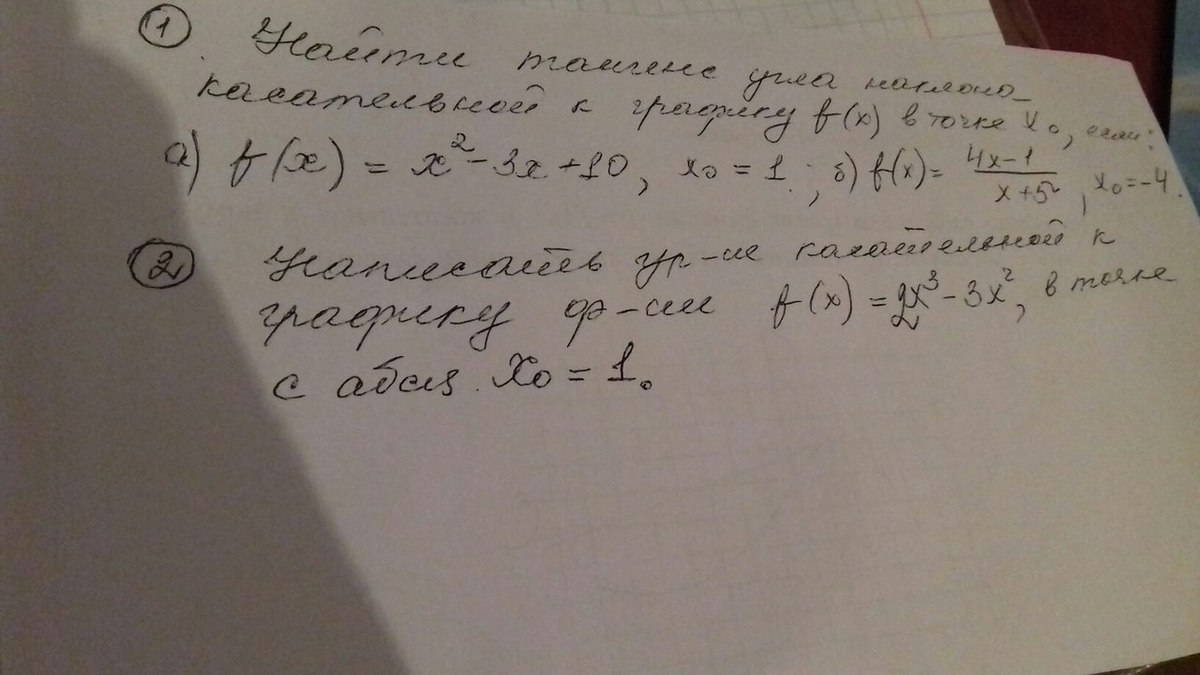
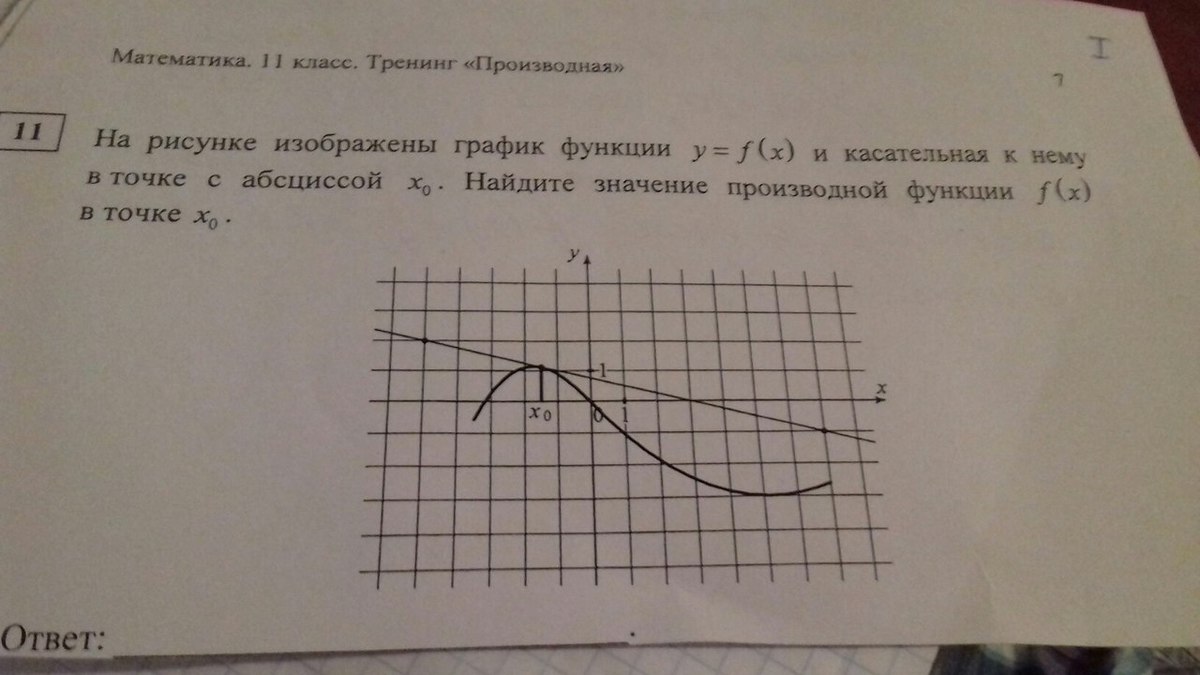
Ответы
Автор ответа:
0
1) y = x^2 - 3x + 10 ;
x0 = 1;
tg Ф= y'(x0) = 2x - 3;
y'(1)= 2*1 - 3 = 2 - 3 = - 1.
tg Ф = -1;
f(x) = (4x-1) / (x+5) ; x0 = - 4.
f '(x)=4*(x+5)-(4x-1)*1/(x+5)^2 = 4x+20-4x + 1 /(x+5)^2=
=21/(x+5)^2;
tgФ= f'(x0);
tgФ= f '(- 4) = 21/(-4+5)^2 = 21/ 1= 21;
2. f(x) = 2x^3 - 3x^2 ; x0 = 1;
f(1)= 2*1^3 - 3*1^2 = - 1;
f '(x) = 6x^2 - 6x;
f '(1) = 6*1^2 - 6*1 = 0;
y = f '(x0)*(x - x0) + f( x0) ;
y = 0*(x -1) + (-1) ;
y = -1 - уравнение касательной
x0 = 1;
tg Ф= y'(x0) = 2x - 3;
y'(1)= 2*1 - 3 = 2 - 3 = - 1.
tg Ф = -1;
f(x) = (4x-1) / (x+5) ; x0 = - 4.
f '(x)=4*(x+5)-(4x-1)*1/(x+5)^2 = 4x+20-4x + 1 /(x+5)^2=
=21/(x+5)^2;
tgФ= f'(x0);
tgФ= f '(- 4) = 21/(-4+5)^2 = 21/ 1= 21;
2. f(x) = 2x^3 - 3x^2 ; x0 = 1;
f(1)= 2*1^3 - 3*1^2 = - 1;
f '(x) = 6x^2 - 6x;
f '(1) = 6*1^2 - 6*1 = 0;
y = f '(x0)*(x - x0) + f( x0) ;
y = 0*(x -1) + (-1) ;
y = -1 - уравнение касательной
Похожие вопросы
Предмет: Математика,
автор: gadjieva2105
Предмет: Литература,
автор: ustugovakristina8
Предмет: Английский язык,
автор: Аноним
Предмет: История,
автор: Пастерна
Предмет: Алгебра,
автор: fot98