Предмет: Геометрия,
автор: Ксюшка23
Меньшая диагональ правильного шестиугольника равна 6√3, найдите длину окружности , описанный около этого шестиугольника.
Объясните, пожалуйста, как это решить.
Ответы
Автор ответа:
0
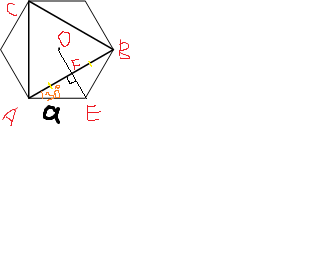
AB=6√3
AF=6√3:2=3√3
AF:AE=COS 30° ⇒ AE=AF : COS 30°=3√3:(√3:2)=6
В правильном шестиугольнике R=сторона шестиугольника
С(длина впис. окр.)=2πR=2*3,14*6=37,68
AF=6√3:2=3√3
AF:AE=COS 30° ⇒ AE=AF : COS 30°=3√3:(√3:2)=6
В правильном шестиугольнике R=сторона шестиугольника
С(длина впис. окр.)=2πR=2*3,14*6=37,68
Приложения:
Автор ответа:
0
AE=OE
Автор ответа:
0
Я СЧИТАЮ ТАК, НО, ВОЗМОЖНО, ОНО НЕ СОВСЕМ ПРАВИЛЬНО
Похожие вопросы
Предмет: История,
автор: ibragimibragimov
Предмет: Қазақ тiлi,
автор: muhtarzanuzakov555
Предмет: Обществознание,
автор: dilnazguttygulova
Предмет: Физика,
автор: lilygrigs
Предмет: Математика,
автор: Ponikarovskaya