Ребят,помогите,плиииз:3
Задание во вложении
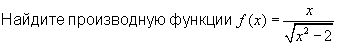
Ответы
f(x) = x / (/(x^2 - 2)).
Используем формулу производной частного:
f '(x) = ( (x)' * /(x^2 - 2) - x * (/(x^2 - 2))' ) / (/(x^2 - 2))^2
Вычислим две производные, содержащиеся в последнем выражении:
1) (x)' = 1
2) (/(x^2 - 2))' Это - производная сложной функции.
(/(x^2 - 2))' = 1/ 2/(x^2 - 2) * (x^2 - 2)' = 2x/ 2/(x^2 - 2) = x/ /(x^2 - 2) .
Итак, продолжим наши рассуждения:
f '(x) = ( (x)' * /(x^2 - 2) - x * (/(x^2 - 2))' ) / (/(x^2 - 2))^2 =
= ( 1 * /(x^2 - 2) - x * x/ /(x^2 - 2) ) / x^2 -2 = ( /(x^2 - 2) / x^2 -2 ) - (x^2 / /((x^2 - 2)^3) ) =
= 1 / /(x^2 - 2) - (x^2 / /((x^2 - 2)^3) ).
Ответ: 1 / /(x^2 - 2) - (x^2 / /((x^2 - 2)^3) ).
В нормальных знаках степеней и корней ответ выйдет не таким уж страшным))
Главное - не запутаться в скобках)
Понравилось решение - поблагодарите)