Question

Катет прямоугольного треугольника равен 8 см, а его проекция на гипотенузу - 4см, Найти гипотенузу.

Answer 1

8*8/4=16 сантиметров.

Answer 2

a^2=b*h, 

8^2=4b

4b=64

b=16

Ответ: 16

Answer 3

Ответ:

16 см.

Объяснение:

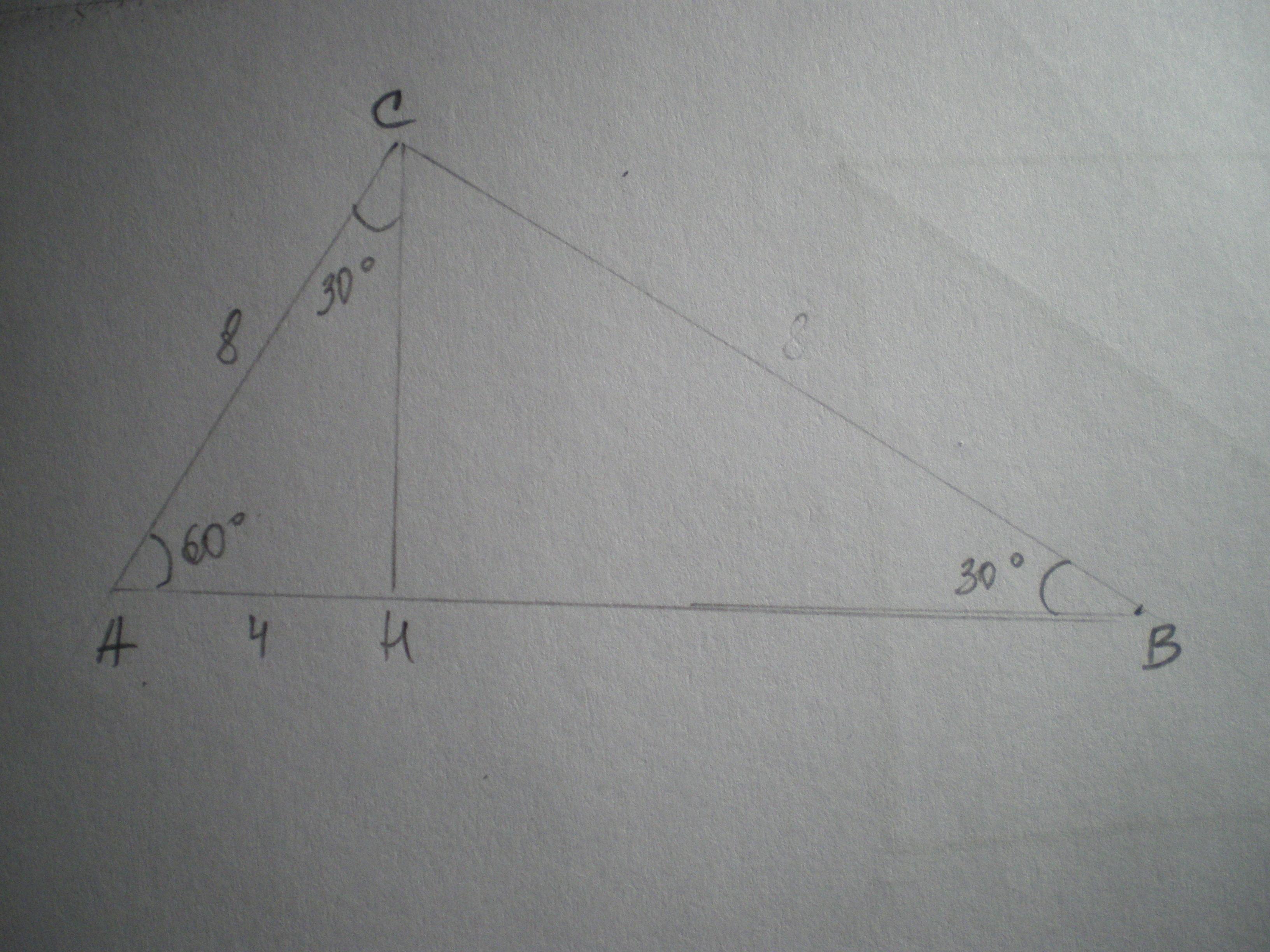
Дано: ΔАВС - прямоугольный, ∠С=90°, АС=8 см, АН=4 см. Найти АВ.

Отрезки гипотенузы, на которые разделяет её высота, являются проекциями катетов.  АН - проекция АС на АВ.  

  Заметим, что в Δ АСН катет АН равен половине гипотенузы АС. В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы. Значит, ∠АСН=30°.

∠АСН=90-30=60°

Сумма острых углов прямоугольного треугольника составляет 90°, поэтому ∠В=90-60=30°.

Следовательно, АВ=2АС=8*2=16 см.

Answer 4

Как известно, квадрат катета равен произведению гипотенузы на проекцию катета на гипотенузу. т.е. 8²=с*4, откуда гипотенуза с=64/4=16/см/