Предмет: Математика,
автор: konalex1
помогите решить неравенство. графически решил, а в теории???
Приложения:
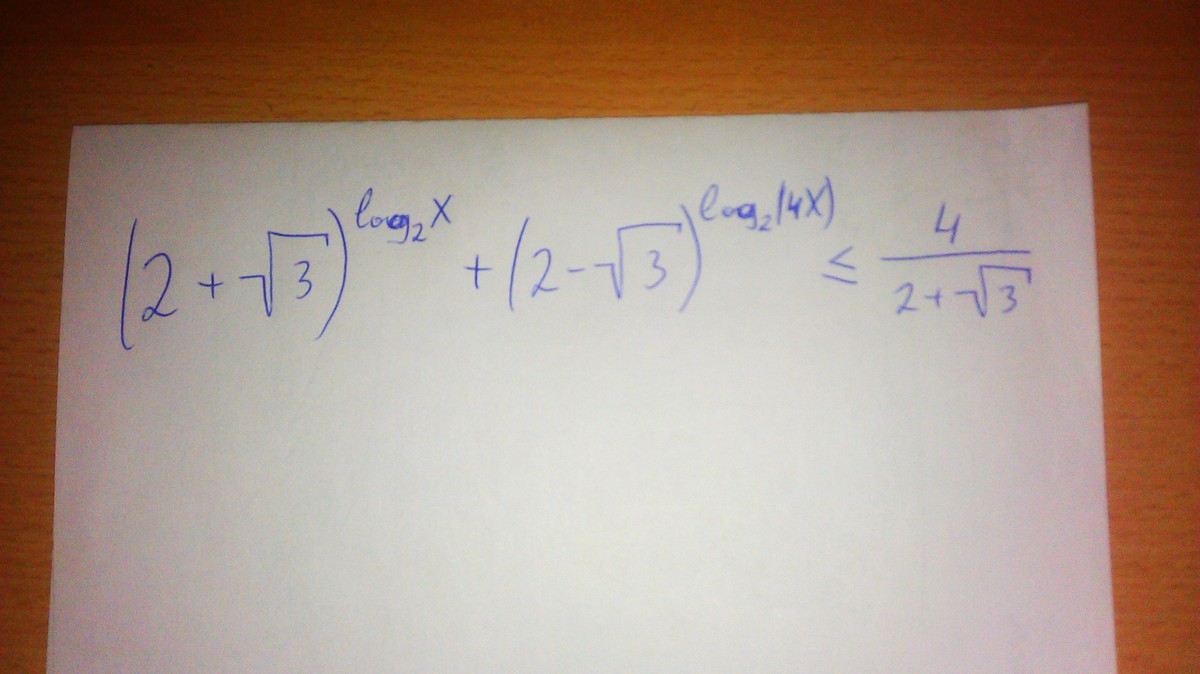
Ответы
Автор ответа:
0
(2+sqrt(3))=a
(2-sqrt(3))=b
ab=1
a^lg2(x)+b^(lg2(x)+2)<=4b
1+b^2(lg2(x))*b^2<=4b*b^lg2(x)
Обозначим b*b^lg2(x)= u
1+u*u<=4u
u*u-4u+1<=0
(u-2)^2<=3
2-sqrt(3)<=u<=2+sqrt(3)
u=(2-sqrt(3))*(2-sqrt(3))^lg2(x)
u=>2-sqrt(3) означает, что (2-sqrt(3))^lg2(x) >1 Что означает х<=1
u<=2+sqrt(3) означает, что (2-sqrt(3))*(2-sqrt(3))^lg2(x)<=2+sqrt(3) или
(2-sqrt(3))*((2-sqrt(3))^(lg2(x)+1))<=1
Что значит :(lg2(x)+1)=>-1
lg2(x)=>-2
x=>1/4
итак: 1/4<=x<=1
(2-sqrt(3))=b
ab=1
a^lg2(x)+b^(lg2(x)+2)<=4b
1+b^2(lg2(x))*b^2<=4b*b^lg2(x)
Обозначим b*b^lg2(x)= u
1+u*u<=4u
u*u-4u+1<=0
(u-2)^2<=3
2-sqrt(3)<=u<=2+sqrt(3)
u=(2-sqrt(3))*(2-sqrt(3))^lg2(x)
u=>2-sqrt(3) означает, что (2-sqrt(3))^lg2(x) >1 Что означает х<=1
u<=2+sqrt(3) означает, что (2-sqrt(3))*(2-sqrt(3))^lg2(x)<=2+sqrt(3) или
(2-sqrt(3))*((2-sqrt(3))^(lg2(x)+1))<=1
Что значит :(lg2(x)+1)=>-1
lg2(x)=>-2
x=>1/4
итак: 1/4<=x<=1
Автор ответа:
0
графическое решение верно. ОДЗ: Х>0
Автор ответа:
0
Больше 1 описался, там указано больше 0. Но 1/4 прка не вижу.
Автор ответа:
0
Впрочем, в 1<=(4b-b^2)*b^lg2(x) кажется ошибка. Слева квадрат в показателе. Сейчас посмотрю.
Автор ответа:
0
Я построил в Excel и получил графическое решение...
Автор ответа:
0
Вы правы! Была ошибка. Исправил. Ваш ответ верен. Но вывод у меня не слишком изящный получился.
Похожие вопросы
Предмет: Химия,
автор: arialnoils
Предмет: Химия,
автор: stoffi
Предмет: Информатика,
автор: marlenserikov801
Предмет: Алгебра,
автор: Аноним
Предмет: История,
автор: ffffhkh