Предмет: Алгебра,
автор: karavanov1
Найдите промежутки возрастание и убывания функции y=f(x):

Это что значит? Что производная не существует? Если продолжу запись, тогда будет: 
Докажите, что данная функция в области определения является возрастающей:

А это значит что возрастающая, т.к. знак неравенства не поменялось?
Ответы
Автор ответа:
0
решение смотри на фотографии
Приложения:
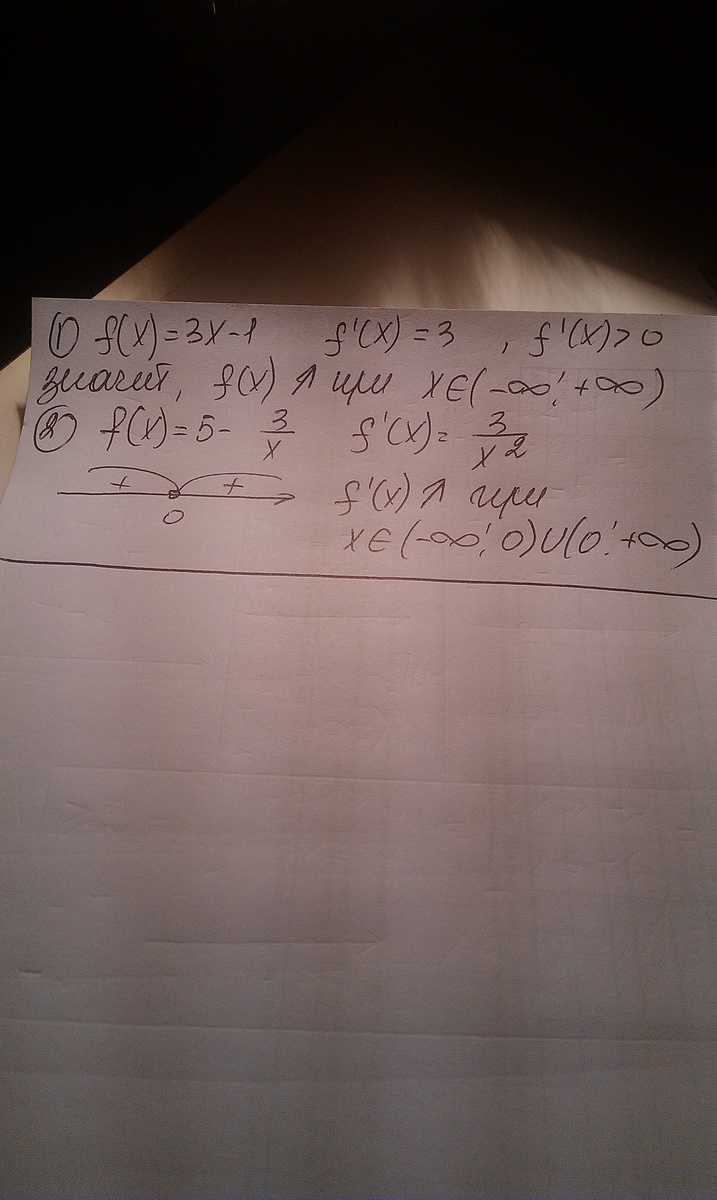
Автор ответа:
0
Спасибо за решение! А в каких случаях или примерах говорят, что производная не существует?
Автор ответа:
0
Аналогичный пример. f(x) = 1,5-2x, f'(x)=-2, f'(x)<0, значит убывает при на минус-плюс бесконечности? Или надо расписать как -2>0 2<0 ? если проверять возрастает ли функция
Автор ответа:
0
если производная отрицательная, то функция убывает от - бесконечности до + бесконечности
Автор ответа:
0
понял. А вопрос выше насчет "когда производная не существует?"
Похожие вопросы
Предмет: Физика,
автор: anarmetovbekzhan
Предмет: Биология,
автор: E4228
Предмет: Математика,
автор: jasmina35l
Предмет: Математика,
автор: Алёнка299829