Предмет: Геометрия,
автор: IFender
Основания трапеции относятся как 3:7. Через точку пересечения диагоналей проведена прямая параллельная основаниям. В каком отношении эта прямая делит площадь трапеции? ВСЕ ОЧЕНЬ ПОДРОБНО С РИСУНКОМ
Ответы
Автор ответа:
0
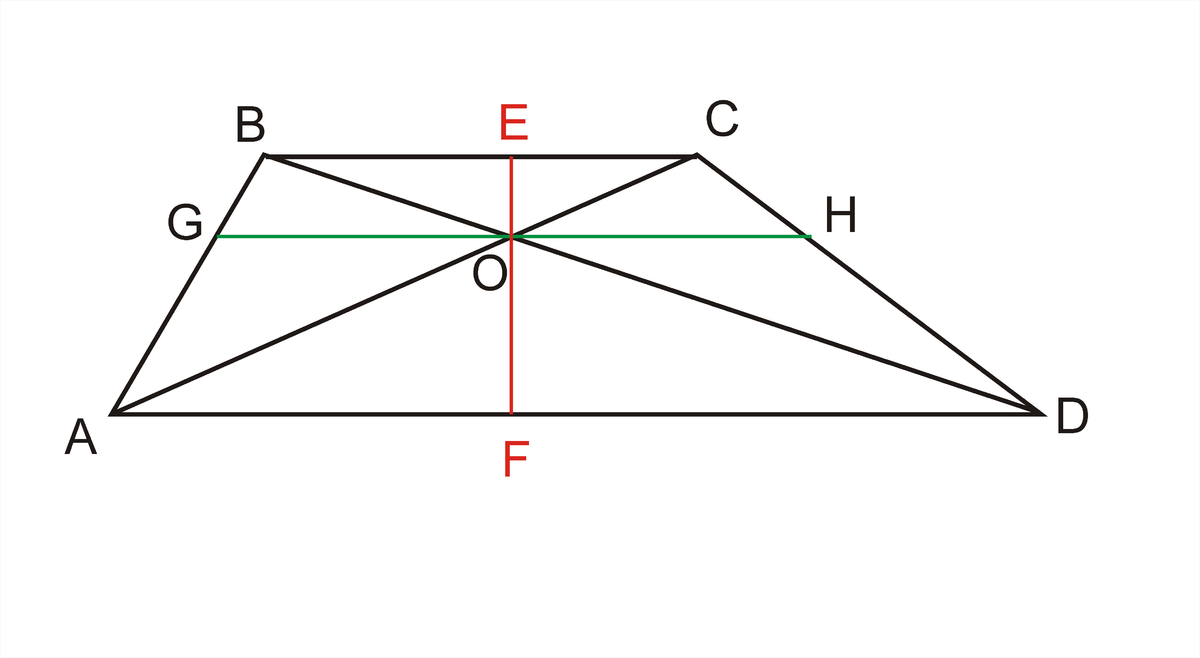
Треугольники AOD и ВОС подобны друг другу.ВС/AD = OC/AO = 3/7
Через точку пересечения диагоналей проведем высоту трапеции EF (на рисунке красным цветом).Углы OAF и OCE равны как внутренние накрест лежащие.Углы AFO и CEO равны 90 градусов (высота перпендикулярна основаниям трапеции).Поэтому эти треугольники подобны.ОС/АО = ОЕ/OF = 3/7.
Пусть меньшее основание трапеции равно 3х, а большее – 7х.Тогда GH = 2*3x*7x/(3x + 7x) = 4,2х.Площадь верхней трапеции GBCH равна:S1 = (BC + GH)*EO/2 = (3x + 4,2x)*EO/2 = 3,6x*EOПлощадь нижней трапеции AGHD равна:S2 = (AD + GH)*OF/2 = (7x + 4,2x)*OF/2 = 5,6x*FO
Искомое соотношение равно S1/S2 = 3,6x*EO/5,6x*FO = (3,6*3)/(5,6*7) = 10,8/39,2 = 108/392 = 54/196
Ответ: 54/196
Через точку пересечения диагоналей проведем высоту трапеции EF (на рисунке красным цветом).Углы OAF и OCE равны как внутренние накрест лежащие.Углы AFO и CEO равны 90 градусов (высота перпендикулярна основаниям трапеции).Поэтому эти треугольники подобны.ОС/АО = ОЕ/OF = 3/7.
Пусть меньшее основание трапеции равно 3х, а большее – 7х.Тогда GH = 2*3x*7x/(3x + 7x) = 4,2х.Площадь верхней трапеции GBCH равна:S1 = (BC + GH)*EO/2 = (3x + 4,2x)*EO/2 = 3,6x*EOПлощадь нижней трапеции AGHD равна:S2 = (AD + GH)*OF/2 = (7x + 4,2x)*OF/2 = 5,6x*FO
Искомое соотношение равно S1/S2 = 3,6x*EO/5,6x*FO = (3,6*3)/(5,6*7) = 10,8/39,2 = 108/392 = 54/196
Ответ: 54/196
Приложения:
Автор ответа:
0
Тогда GH = 2*3x*7x/(3x + 7x) а откуда это? почему так?
Автор ответа:
0
Согласно теореме Буракова. В школьном учебнике она формулируется так: отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей трапеции, равен среднему гармоническому длин ее оснований: 2ху/(х+у), где х и у - основания трапеции. В случае необходимости могу предоставить доказательство.
Похожие вопросы
Предмет: Кыргыз тили,
автор: gmailcomhasbeen
Предмет: Українська мова,
автор: kunak81
Предмет: Математика,
автор: ksuxavolk10
Предмет: Обществознание,
автор: mariyasokolova