Предмет: Алгебра,
автор: evgen2evgen
решите уравнение желательно с объяснениями
Приложения:
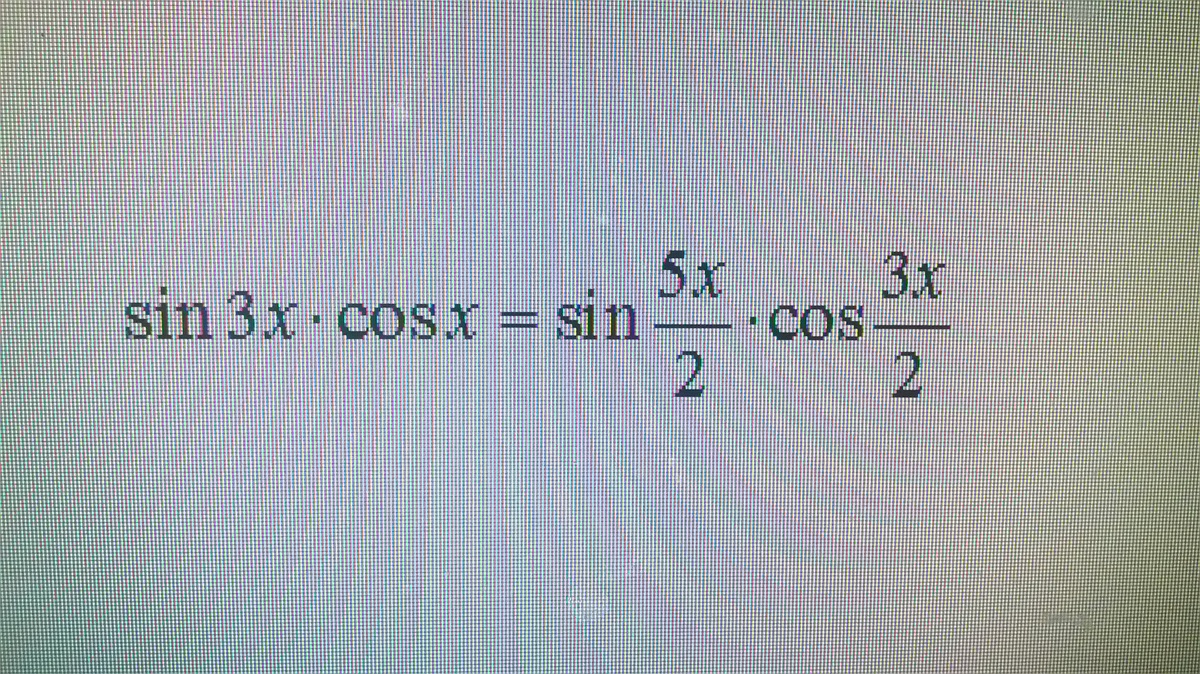
Ответы
Автор ответа:
0
Посмотрим в отдельности на правую и левую части уранвения:
Sin3xCosx = 1/2(Sin4x +Sin2x);
Sin5x/2 Cos3x/2 = 1/2(Sin4x +Sinx)
Итак, наше уравнение выглядит:
1/2(Sin4x +Sin2x) = 1/2(Sin4x +Sinx)
Sin4x + Sin2x = Sin4x +Sinx
Sin2x - Sinx = 0
2SinxCos x - Sinx = 0
Sinx(2Cosx -1) = 0
Sinx = 0 или 2Сosx -1 = 0
x = πn, n ∈Z Cos x = 1/2
x = +- π/3 + 2πk , k ∈Z
Sin3xCosx = 1/2(Sin4x +Sin2x);
Sin5x/2 Cos3x/2 = 1/2(Sin4x +Sinx)
Итак, наше уравнение выглядит:
1/2(Sin4x +Sin2x) = 1/2(Sin4x +Sinx)
Sin4x + Sin2x = Sin4x +Sinx
Sin2x - Sinx = 0
2SinxCos x - Sinx = 0
Sinx(2Cosx -1) = 0
Sinx = 0 или 2Сosx -1 = 0
x = πn, n ∈Z Cos x = 1/2
x = +- π/3 + 2πk , k ∈Z
Автор ответа:
0
1/2(Sin4x +Sin2x)-как это получили,по формуле? по формуле двойного угла?
Автор ответа:
0
2Sinα Cosß = Sin(α + ß) + Sin(α - ß)
Похожие вопросы
Предмет: История,
автор: nunishnasirova
Предмет: Математика,
автор: 1KoKoSiK1
Предмет: Химия,
автор: egamovanargiza67
Предмет: Алгебра,
автор: kkomleva
Предмет: Математика,
автор: Димзомб12