Предмет: Алгебра,
автор: Vladimir654
Найдите наибольшее и наименьшее значения функции на промежутке [-5;-2]
Приложения:
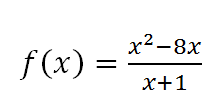
Ответы
Автор ответа:
0
Найдём f'(x)=((x^2-8x)' * (x+1) - (x^2-8x) * (x+1)')/(x+1)^2. f'(x) = ((2x-8)(x+1) - x^2-8x)/(x^2-1)^2= x^2+2x-8/(x-1)^2. Теперь приравниваем производную к нулю: x^2+2x-8=0 d=36 X1=2 x2=-4. Знаменатель: x+1!=0 x!=-1. Осталось вычислить: f(-5)= 25+40/-4 = -16,25. f(-4) = 16+32/-3=-16. f(-2)= 4+16/-1 = -20. f(2) не вычисляем, так как значение не попало в промежуток. Получаем, что наим= -20 наиб= -16
Автор ответа:
0
Огромное спасибо
Автор ответа:
0
Не за что
Похожие вопросы
Предмет: Алгебра,
автор: tkacevaviktoria60
Предмет: Другие предметы,
автор: lIakcl
Предмет: Физкультура и спорт,
автор: ulianaermakova
Предмет: Математика,
автор: Анютка101
Предмет: Математика,
автор: лизик654