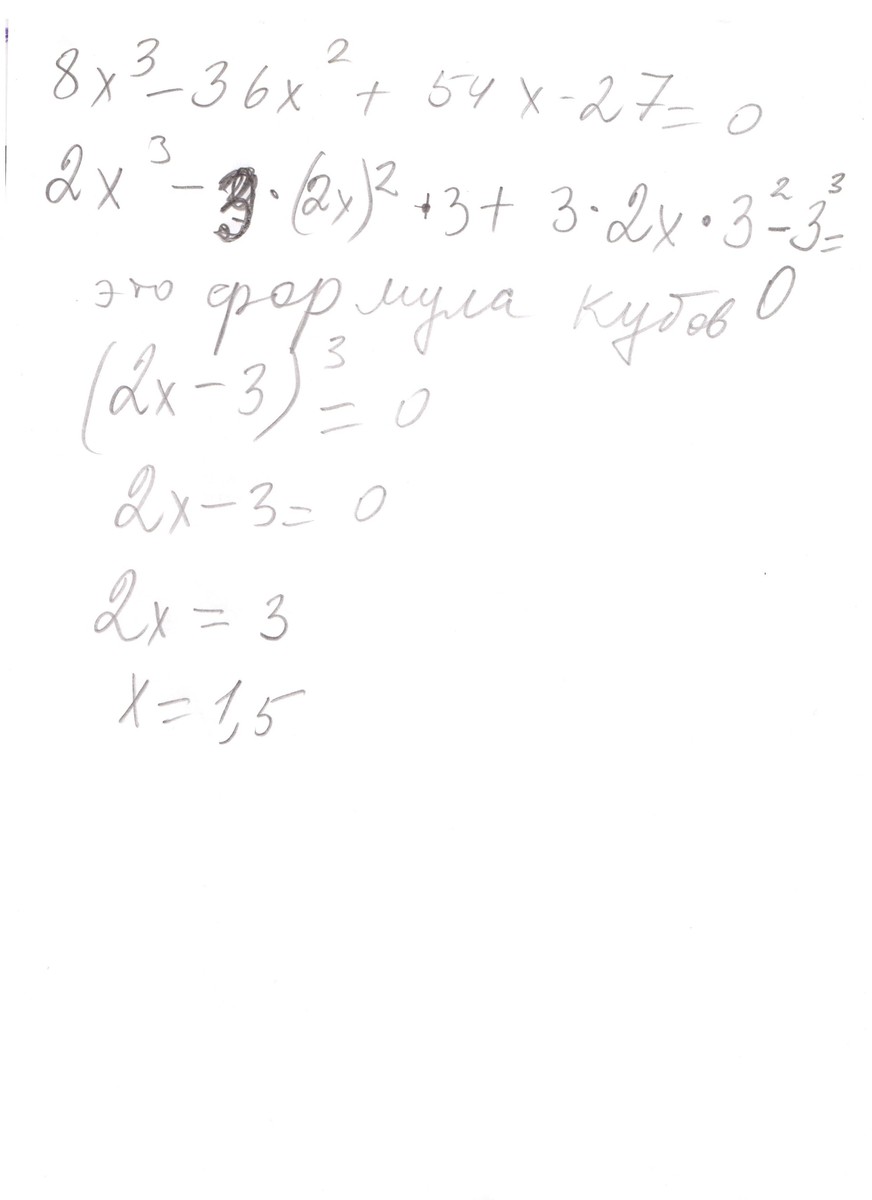Помогите решить 2 задания по алгебре 7 класс
Задания 7 и 8
ответы даны во 2 файле , нужно подробное решение
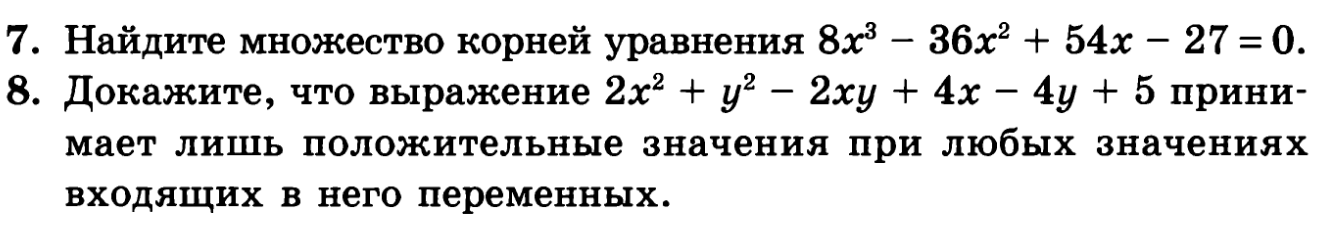
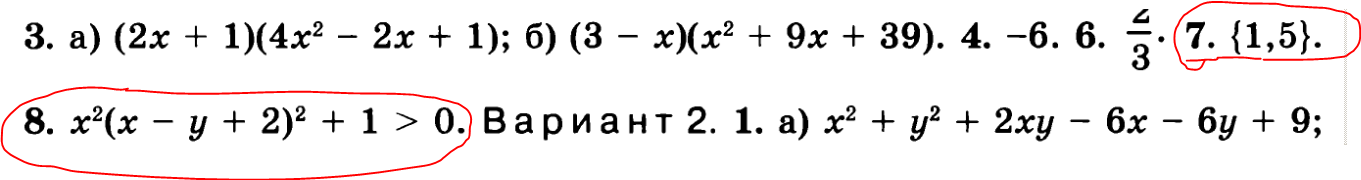
Ответы
если видна формула куба разности , то
если нет, то
</var></p>
<p> </p>
<p>Второе задание (с помощью выделения квадрата выражения)</p>
<p><img src=[/tex]2x^2+y^2-2xy+4x-4y+5=\\ x^2+y^2+x^2+2^2-2*x*y+2*2*x-2*2*y+1=\\ x^2+(x-y+2)^2+1 geq 0+0+1=1>0;" title="8x^3-36x^2+54x-27=0;\\8x^3-12x^2-24x^2+36x+18x-27=0;\\(8x^3-12x^2)-(24x^2-36x)+(18x-27)=0;\\4x^2(2x-3)-12x(2x-3)+9(2x-3)=0;\\(4x^2-12x+9)(2x-3)=0;\\(2x-3)^2(2x-3)=0;\\(2x-3)^3=0;\\2x-3=0;\\2x=3;\\x=1.5" title="2x^2+y^2-2xy+4x-4y+5=\\ x^2+y^2+x^2+2^2-2*x*y+2*2*x-2*2*y+1=\\ x^2+(x-y+2)^2+1 geq 0+0+1=1>0;" title="8x^3-36x^2+54x-27=0;\\8x^3-12x^2-24x^2+36x+18x-27=0;\\(8x^3-12x^2)-(24x^2-36x)+(18x-27)=0;\\4x^2(2x-3)-12x(2x-3)+9(2x-3)=0;\\(4x^2-12x+9)(2x-3)=0;\\(2x-3)^2(2x-3)=0;\\(2x-3)^3=0;\\2x-3=0;\\2x=3;\\x=1.5" alt="2x^2+y^2-2xy+4x-4y+5=\\ x^2+y^2+x^2+2^2-2*x*y+2*2*x-2*2*y+1=\\ x^2+(x-y+2)^2+1 geq 0+0+1=1>0;" title="8x^3-36x^2+54x-27=0;\\8x^3-12x^2-24x^2+36x+18x-27=0;\\(8x^3-12x^2)-(24x^2-36x)+(18x-27)=0;\\4x^2(2x-3)-12x(2x-3)+9(2x-3)=0;\\(4x^2-12x+9)(2x-3)=0;\\(2x-3)^2(2x-3)=0;\\(2x-3)^3=0;\\2x-3=0;\\2x=3;\\x=1.5" />
Второе задание (с помощью выделения квадрата выражения)
Второе задание (с помощью выделения квадрата выражения)
так как квадрат любого выражения неотрицателен,сумма неотрицательного и положительного положительное
+ формула квадрата тричлена
[tex](a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc" title="2x^2+y^2-2xy+4x-4y+5=\\ x^2+y^2+x^2+2^2-2*x*y+2*2*x-2*2*y+1=\\ x^2+(x-y+2)^2+1 geq 0+0+1=1>0;" />
так как квадрат любого выражения неотрицателен,сумма неотрицательного и положительного положительное
+ формула квадрата тричлена
[tex](a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc" alt="2x^2+y^2-2xy+4x-4y+5=\\ x^2+y^2+x^2+2^2-2*x*y+2*2*x-2*2*y+1=\\ x^2+(x-y+2)^2+1 geq 0+0+1=1>0;" />
так как квадрат любого выражения неотрицателен,сумма неотрицательного и положительного положительное
+ формула квадрата тричлена
[tex](a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc" />
сммммммммотри вложения в 1 заданиии разложи по формуле разность кубов
2 задание находим квадрат выражения
и получится в ответе
х²(х-у+2)²+1>0
ввторой раз переделываююю так плохо копирует принтер