Задания во вложениях :с прошу помогите!!!!!

Ответы
Двугранный угол - это угол между плоскостями. Величина двугранного угла равна величине линейного угла с вершиной на линии пересечения плоскостей, стороны которого перпендикулярны ребру двугранного угла (линии пересечения плоскостей).
№1.
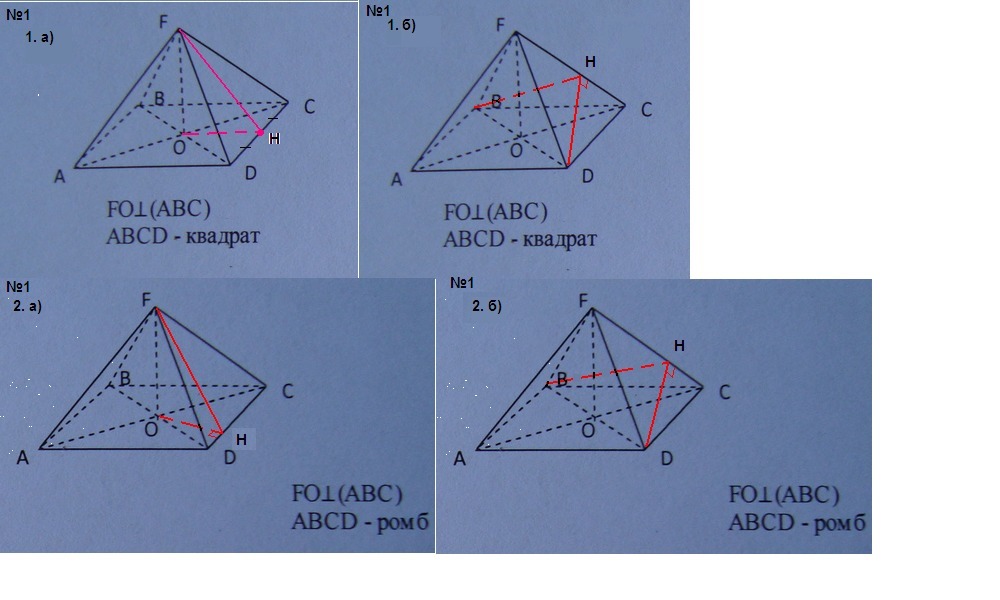
1. Пирамида с квадратом в основании.
а) Угол между плоскостями (АВС) и (FDC):
Плоскости пересекаются по прямой DC, значит DC - ребро двугранного угла.
Так как основание пирамиды - квадрат, а высота проецируется в центр основания, пирамида правильная. Тогда боковые грани - равные равнобедренные треугольники.
Пусть Н - середина DC, тогда FH - медиана, а значит и высота равнобедренного треугольника FDC, а ОН - медиана, а значит и высота равнобедренного треугольника DOC (диагонали квадрата равны и точкой пересечения делятся пополам).
Итак, FH⊥DC, OH⊥DC, значит
∠FHO - линейный угол двугранного угла между плоскостями (АВС) и (FDC).
Так как в этой и остальных задачах нет никаких числовых данных, то, вероятно, речь идет о построении линейного угла.
б) Угол между плоскостями (FDC) и (FBC):
Плоскости пересекаются по прямой FC - это ребро двугранного угла.
Проведем DH⊥FC.
DC = ВС как стороны квадрата, ∠DCH = ∠BCH так как боковые грани - равные треугольники, СН - общая сторона для треугольников DCH и ВСН, ⇒ они равны по двум сторонам и углу между ними, значит ВН⊥FC.
Итак, DH⊥FC, BH⊥FC, значит
∠DHB - линейный угол между плоскостями (FDC) и (FBC).
2. Пирамида с ромбом в основании.
а) Угол между плоскостями (АВС) и (FDC):
Плоскости пересекаются по прямой DC, значит DC - ребро двугранного угла.
Проведем ОН⊥DC. ОН - проекция наклонной FH на плоскость (АВС), значит FH⊥DC по теореме о трех перпендикулярах.
Итак, ОН⊥DC, FH⊥DC, ⇒
∠FHO - линейный угол двугранного угла между плоскостями (АВС) и (FDC).
б) Угол между плоскостями (FDC) и (FBC):
Плоскости пересекаются по прямой FC - это ребро двугранного угла.
Проведем DH⊥FC. Докажем, что и ВН⊥DC.
ΔBFD равнобедренный, так как в нем FO - высота и медиана,
FB = FD,
DC = BC как стороны ромба,
FC - общая сторона для треугольников DFC и BFC, значит они равны по трем сторонам. Значит ∠FCD = ∠FCB.
Тогда в треугольниках DCH и ВСН:
∠DCH = ∠ВСН как доказано выше,
DC = BC как стороны ромба,
НС - общая сторона,
тогда треугольники равны по двум сторонам и углу между ними.
Значит и ВН⊥FC.
Итак, DH⊥FC, BH⊥FC, ⇒
∠DHB - линейный угол между плоскостями (FDC) и (FBC).
№2.
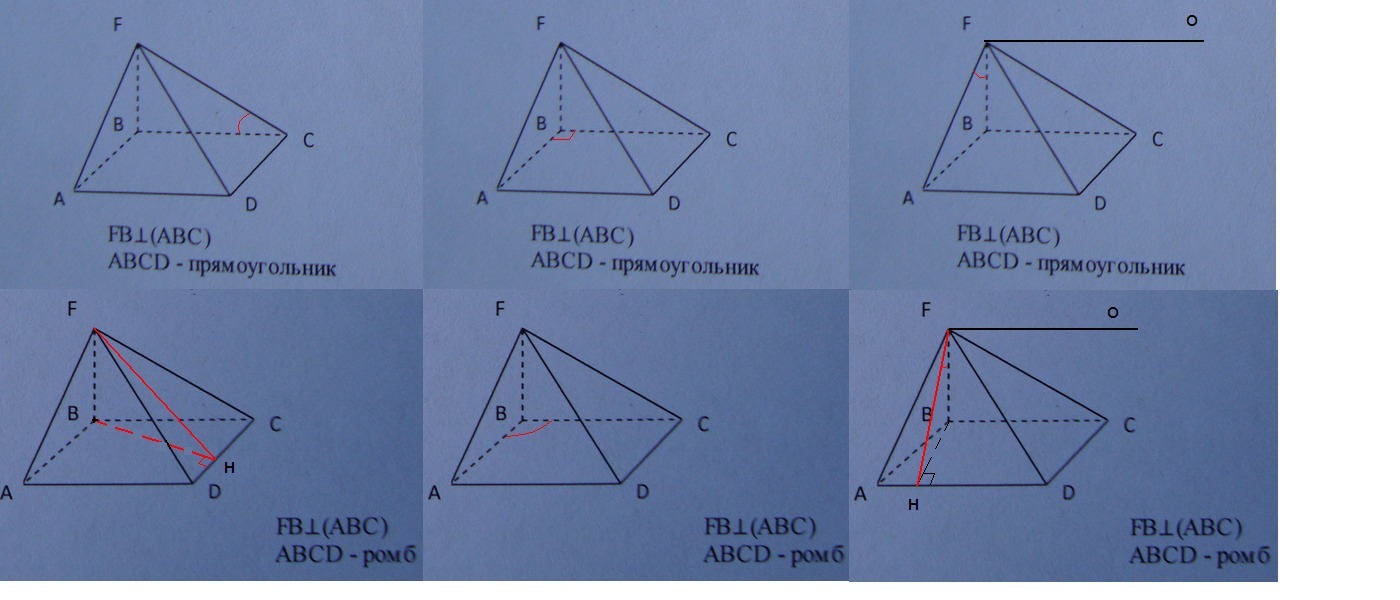
1. Пирамида с прямоугольником в основании.
а) Угол между плоскостями (АВС) и (FDC).
(АВС) ∩ (FDC) = DC - ребро двугранного угла.
ВС⊥DC как смежные стороны прямоугольника, ВС - проекция наклонной FC на плоскость (АВС), значит FC⊥DC по теореме о трех перпендикулярах.
Итак, BC⊥DC, FC⊥DC, ⇒
∠FCB - линейный угол двугранного угла между плоскостями (АВС) и (FDC).
б) Угол между плоскостями (AFB) и (FBC).
(AFB) ∩ (FBC) = FB.
Если прямая перпендикулярна плоскости, то она перпендикулярна каждой прямой, лежащей в этой плоскости, значит
AB⊥FB, CB⊥FB, ⇒
∠АВС - линейный угол двугранного угла между плоскостями (AFB) и (FBC).
в) Угол между плоскостями (AFD) и (FBC).
AD║ВС, значит AD параллельна плоскости (FBC).
Плоскость (FDC) проходит через AD и пересекает плоскость (FBC), значит линия пересечения плоскостей параллельна AD. Пусть это прямая FO.
FB⊥BC, ⇒ FB⊥FO;
АВ⊥ВС и АВ⊥FB, значит АВ⊥(FBC), тогда
FB - проекция наклонной AF на плоскость FBC, значит и AF⊥FO по теореме о трех перпендикулярах. Тогда
∠AFB линейный угол двугранного угла между плоскостями (AFD) и (FBC).
2. Пирамида с ромбом в основании.
а) Угол между плоскостями (АВС) и (FDC).
(АВС) ∩ (FDC) = DC - ребро двугранного угла.
Проведем ВН⊥DC, ВН - проекция FH на плоскость (АВС), значит и FH⊥DC по теореме о трех перпендикулярах. Тогда
∠FHB - линейный угол между плоскостями (АВС) и (FDC).
б) Угол между плоскостями (AFB) и (FBC).
(AFB) ∩ (FBC) = FB.
Если прямая перпендикулярна плоскости, то она перпендикулярна каждой прямой, лежащей в этой плоскости, значит
AB⊥FB, CB⊥FB, ⇒
∠АВС - линейный угол двугранного угла между плоскостями (AFB) и (FBC).
в) Угол между плоскостями (AFD) и (FBC).
AD║ВС, значит AD параллельна плоскости (FBC).
Плоскость (FDC) проходит через AD и пересекает плоскость (FBC), значит линия пересечения плоскостей параллельна AD. Пусть это прямая FO.
FB⊥BC, ⇒ FB⊥FO;
Проведем НВ⊥ВС. Так как НВ перпендикулярна и FB, то
НВ⊥(FBC), тогда НВ - проекция наклонной FH на плоскость (FBC), значит FH⊥BC, а значит и FH⊥FO по теореме о трех перпендикулярах.
Итак, FB⊥FO, FH⊥FO, ⇒
∠HFB - линейный угол двугранного угла между плоскостями (AFD) и (FBC).