Предмет: Алгебра,
автор: Sherline
Помогите, пожалуйста, решить задания
Приложения:
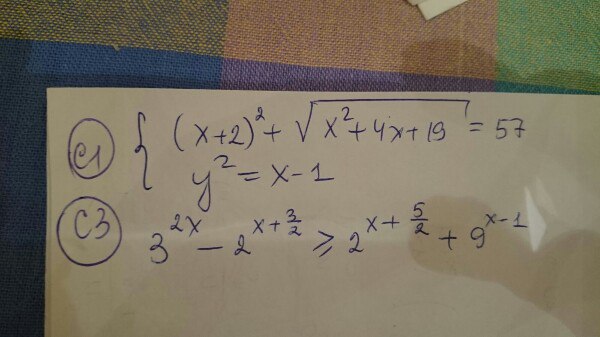
Ответы
Автор ответа:
0
C1.

ОДЗ:
x²+4x+15≥0
(x+2)²+15≥0
Неравенство выполняется при любом х.
Пусть а=(x+2)²

ОДЗ:
a+15≥0
a≥ -15
57-a≥0
-a≥ -57
a ≤ 57
a∈[-15; 57]
a+15=(57-a)²
a+15=3249-114a+a²
-a²+a+114a+15-3249=0
-a² +115a - 3234=0
a² - 115a + 3234=0
D=115² -4*3234=13225-12936=289
a₁=
a₂=
а=66 - не подходит по ОДЗ.
(x+2)²=49
(x+2)² - 7² =0
(x+2-7)(x+2+7)=0
(x-5)(x+9)=0
x-5=0
x=5
x+9=0
x= -9
При х=5
у² = 5-1
у² =4
у₁=2
у₂= -2
При х= -9
у² = -9-1
у²= -10
нет решений.
Ответ: (5; -2)
(5; 2)
C3.


x∈[1.5; +∞)
Ответ: [1.5; +∞)
ОДЗ:
x²+4x+15≥0
(x+2)²+15≥0
Неравенство выполняется при любом х.
Пусть а=(x+2)²
ОДЗ:
a+15≥0
a≥ -15
57-a≥0
-a≥ -57
a ≤ 57
a∈[-15; 57]
a+15=(57-a)²
a+15=3249-114a+a²
-a²+a+114a+15-3249=0
-a² +115a - 3234=0
a² - 115a + 3234=0
D=115² -4*3234=13225-12936=289
a₁=
a₂=
а=66 - не подходит по ОДЗ.
(x+2)²=49
(x+2)² - 7² =0
(x+2-7)(x+2+7)=0
(x-5)(x+9)=0
x-5=0
x=5
x+9=0
x= -9
При х=5
у² = 5-1
у² =4
у₁=2
у₂= -2
При х= -9
у² = -9-1
у²= -10
нет решений.
Ответ: (5; -2)
(5; 2)
C3.
x∈[1.5; +∞)
Ответ: [1.5; +∞)
Похожие вопросы
Предмет: Английский язык,
автор: strikeproblock21
Предмет: История,
автор: surupovaaleksandra87
Предмет: Английский язык,
автор: Аноним
Предмет: Физика,
автор: geibcnbr24