Question

Помогите решить задачу)
Диагональ боковой грани правильной треугольной призмы равна L и образует с плоскостью основания угол α. Найдите площадь боковой поверхности призмы.

Answer 1

если призма правильная треугольная, значит в основании правильный треугольник ( равносторонний), следовательно боковые гранипризмы равны,отсюда находим площадь боковой поверхности...
S=h×P(oснования)
h=sin(a)×L
P=cos(a)×3×L
S=3×L^2×sin(a)×cos(a)

Answer 2

это верное решение

Answer 3

спасибо,а рисунок можно?

Answer 4

простите , но пока я не могу скинуть рисунок, но рисуйте обычную прямую призуму( бок. ребра перпенд.основанию) а в основании равносторлнний треугольник.

Answer 5

ок

Answer 6

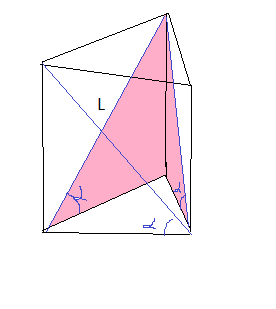
В основании правильной треугольной призмы лежит равносторонний  треугольник.
Боковые ребра призмы перпендикулярны плоскости основания.
Все боковые грани - равные между собой прямоугольники.
Диагональ прямоугольника разбивает его на два равных прямоугольных треугольника ( отмечены на рисунке розовым цветом)

Из прямоугольного треугольника
H=L·sinα
a=L·cosα

S=3·a·H=3·L·cosα·L·sinα=3L²·sin2α/2