Question

Найдите точку минимума функции у= х^3-6х^2+9х-4 пооомооогитееее!

Answer 1

у= х^3-6х^2+9х-4 
y' = 3x^2 - 12x + 9
y' = 0;       3x^2 - 12x + 9 = 0 /3
x^2 - 4x +3 = 0
D = 4 - 3 = 1     D > 0 из этого следует 2 корня
X1 = 2 - 1 = 1 
X2 = 2 + 1 = 3
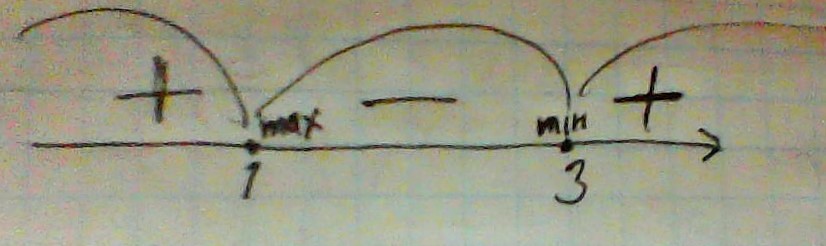
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков.
Ответ: 3