Question

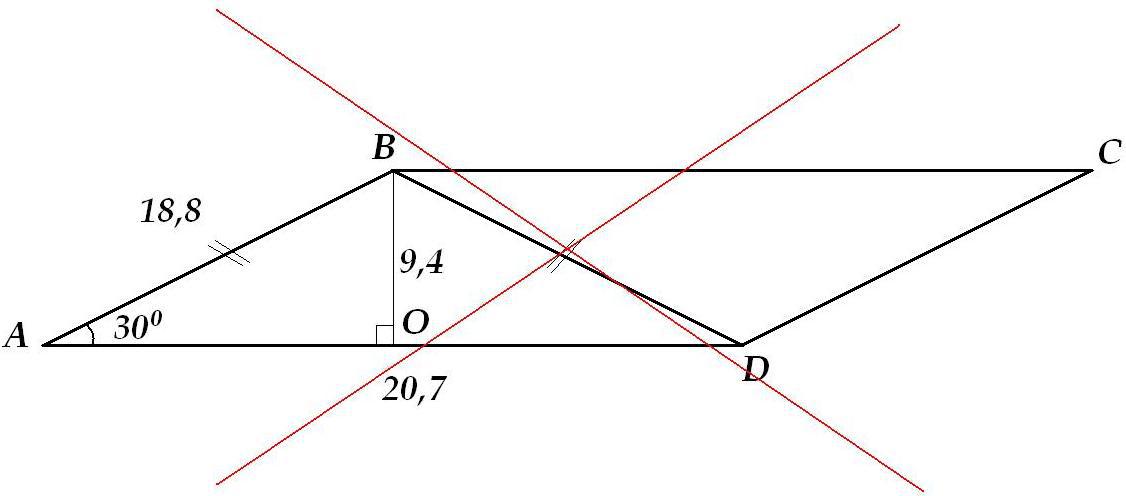
в параллелограмме диагональ BD 18,8 см и она равна стороне AB а угол A 30 градусов,Найдите площадь пароллеограмма если сторона AD 20,7 см

Answer 1

Вся беда в том, что данный параллелограмм не имеет ну вообще никаких шансов на существование )))
С точки зрения простого обывателя решение будет таким:
Высота параллелограмма ВО - это катет, лежащий против угла в 30°, значит равен половине гипотенузы, то есть АВ:

$BO= frac{AB}{2}=frac{18,8}{2}=9,4$ см

$S=ADcdot BO=20,7cdot9,4=194,58$ см²

Что ж, казалось бы, всё безупречно. Но...
Мало-мальски грамотный математик сразу же заметит лажу:
ВО - высота и медиана ΔABD

$AO=OD= frac{AD}{2}=frac{20,7}{2}=10,35$ см

$10,35^2+9,4^2 neq 18,8^2\\107,1225+88,36 neq 354,44\\195,4825 neq 354,44$

По условию этого задания равенство диагонали и боковой стороны вообще никаким боком не нужно, достаточно знать угол 30° и две стороны.
AD в этом случае должно быть равно: AD≈32,56 см
Ну или  AD=20,7 см, но АВ не 18,8, а совсем другой величины, лень считать )) 

...А модераторов попрошу воздержаться от удаления данного задания: в таком виде оно могло быть дано в учебнике, и подобный разбор задания в классе может быть весьма полезен. ))