Question

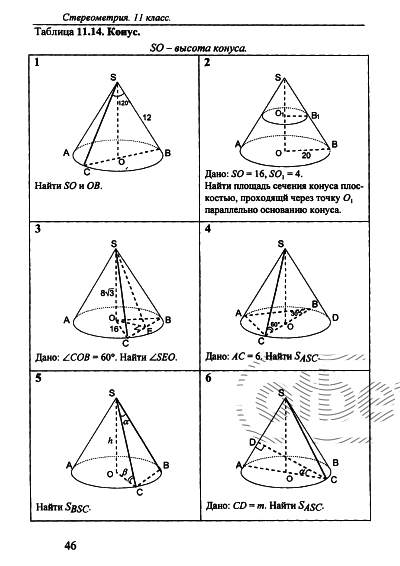
Помогите решить задачи под номерами 1,3,5. Буду благодарен!

Answer 1

Вот первая:
△SOB - прямоугольный, ∠SOB = 90°, ∠OSB = 1/2 ∠CSB = 120°/2 = 60°.
По теореме про сумму углов треугольника ∠SBO = 90° - ∠OSB = 90° - 60° = 30°.
По свойству прямоугольных треугольников если ∠SBO = 30°, то SO = 1/2 SB = 12/2 = 6, SO = 6.
По теореме Пифагора OB = √SB² - SO² = √12² - 6² = √108 = √36 x 3 = 6√3, OB = 6√3
Ответ: 6; 6√3.

Вот третья:
∠COB = 60° ⇒ △COB - правильный, высота правильного треугольника OE = $frac{ sqrt{3}}{2} a$ = 16*√3/2 = 8√3.
△SOE - прямоугольный, tg ∠SEO = SO/OE = 8√3 / 8√3 = 1 ⇒ ∠SEO = 45°.
Ответ: 45°.

Вот пятая:
Площадь искомого треугольника $S_{SBC} = frac{1}{2}SB*SC * sin alpha$, но так как SB = SC (как образуемые), то формула выглядит $S_{SBC}= frac{1}{2} SC^{2}*sin alpha$.
SO = h, sin β = h / SC, SC = h / sin β.
Подставим в формулу: $S_{SBC} = frac{1}{2}( frac{h}{sin beta})^2*sin alpha$.
Ответ: $S_{SBC} = frac{1}{2}( frac{h}{sin beta})^2*sin alpha$.