Question

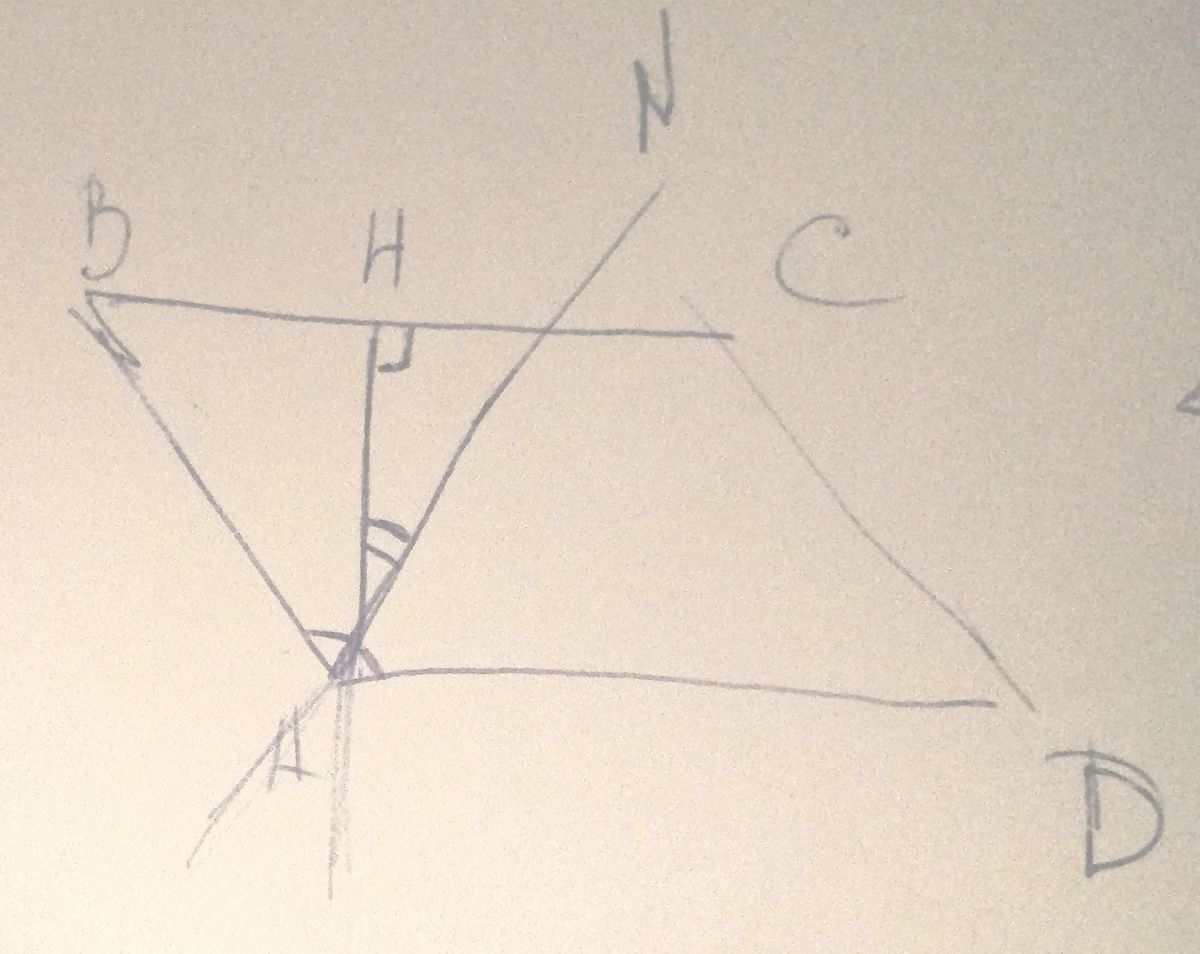
ABCD - параллелограмм ∠HAN = 17, AH-высота, AN - биссектриса угла А,             ∠ABC = ?

Answer 1

∠NAD=∠HNA,т.к  AN секущая при параллельно прямых AD и BC. Рассмотрим ΔHNA. Он прямоугольный. ∠HNA=180°-90°-17°=73°, т.е. ∠NAD=73°. Т.к.AN-биссектриса угла BAD, то ∠NAD=∠NAB=73°. В ΔABN ∠ABN=180°-∠BAC-∠BNA=180°-2·73°=34°. Т.к. ∠ABN=∠ABC, то ∠ABC=34°. Ответ: ∠ABC=34°.
Вар.2.
∠АВС=180°-∠ВАD,∠BAD=2∠NAD. ∠NAD=90°-17°=73°, т.е. ∠BAD=73°·2=146°. Итак, ∠ABC=180°-146°=34°.