Предмет: Геометрия,
автор: Аноним
Хорда двух пересекающихся окружностей является стороной правильного треугольника, вписанного в одну из окружности, и стороной квадрата, вписанного вторую окружность. Длина хорды равна 6√3 см. Найдите расстояние между центрами данных окружностей .
Ответы
Автор ответа:
0
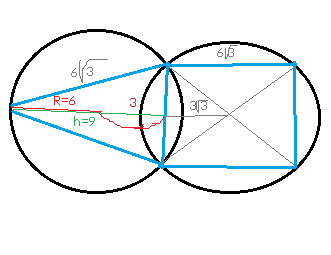
См. рисунок и решение на рисунке
Высота равностороннего треугольника
h=6√3·cos 30°=6√3·√3/2=9 cм

d=h-R=3 cм - расстояние от центра окружности, в которую вписан треугольник до данной хорды
Расстояние от центра окружности, в которую вписан квадрат, до данной хорды равно половине стороны квадрата
Ответ. 3+3√3 ( см)
Высота равностороннего треугольника
h=6√3·cos 30°=6√3·√3/2=9 cм
d=h-R=3 cм - расстояние от центра окружности, в которую вписан треугольник до данной хорды
Расстояние от центра окружности, в которую вписан квадрат, до данной хорды равно половине стороны квадрата
Ответ. 3+3√3 ( см)
Приложения:
Похожие вопросы
Предмет: История,
автор: tema18068
Предмет: Алгебра,
автор: maxchat8317
Предмет: Английский язык,
автор: anelaalieva22
Предмет: Алгебра,
автор: ник1124
Предмет: Геометрия,
автор: Simlich