Question

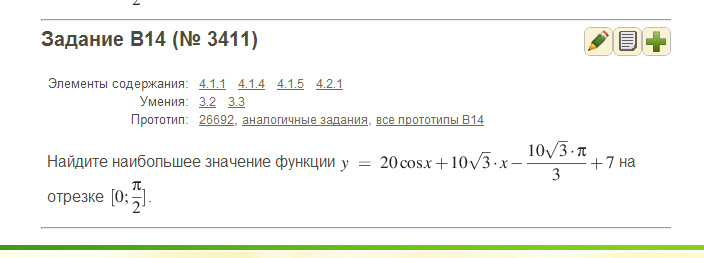
Ребят,помогите,очень прошу. Задание ЕГЭ Фото вложено:****

Answer 1

производную найти надо 

Answer 2

Чтобы найти наибольшее значение на отрезке, нужно найти экстремумы функции и сравнить их со значенями функции на концах отрезка. Подозрительные на экстремум точки - это точки, в которых производная функции равна нулю. Найдем производную и выясним, в каких точках она равна нулю.

$y=20cosx+10sqrt{3}x-frac{10sqrt{3}pi}{3}+7\ y'=(20cosx+10sqrt{3}x-frac{10sqrt{3}pi}{3}+7)='\ =(20cosx)'+(10sqrt{3}x)'-(frac{10sqrt{3}pi}{3})'+7')'=\ =-20sinx+10sqrt{3}-0+0=-20sinx+10sqrt{3}=\ =-10(2sinx-sqrt{3})$

Выясним в каких точках производная равна нулю.

$-10(2sinx-sqrt{3})=0\ 2sinx-sqrt{3}=0\ 2sinx=sqrt{3}\ sinx=frac{sqrt{3}}{2}\ x=(-1)^n arcsin frac{sqrt{3}}{2}+pi n, n E Z\ x=(-1)^n frac{pi}{3}+pi n, n E Z$

В условиях задачи задан отрезок [0;п/2], поэтому нам нужно выбрать только значения из этого промежутка. Этому условию удовлетворяет только точка x=п/3.

Найдем значение функции в этой точке:

$y(frac{pi}{3})=20cos(frac{pi}{3})+10sqrt{3}*frac{pi}{3}-frac{10sqrt{3}pi}{3}+7=\ =20*frac{1}{2}+7=17$

 

Найдем значения функции на концах отрезка:

$y(0)=20cos0+10sqrt{3}*0-frac{10sqrt{3}pi}{3}+7=\ =20*1+0-frac{10sqrt{3}pi}{3}+7=\ =27-frac{10sqrt{3}pi}{3}$

$y(frac{pi}{2})=20cos(frac{pi}{2})+10sqrt{3}*frac{pi}{2}-frac{10sqrt{3}pi}{3}+7=\ =0+frac{10sqrt{3}pi}{6}+7=\ =7+frac{10sqrt{3}pi}{6}$

Выбираем максимальное из трех значений

это 17