Предмет: Геометрия,
автор: Аноним
Номер 11 пожалуйста)))))))))
Приложения:

Ответы
Автор ответа:
0
Не обратила поначалу внимание на номер задачи во вложении.
. Решение задачи 11 ниже.
---------------
Задача 12.
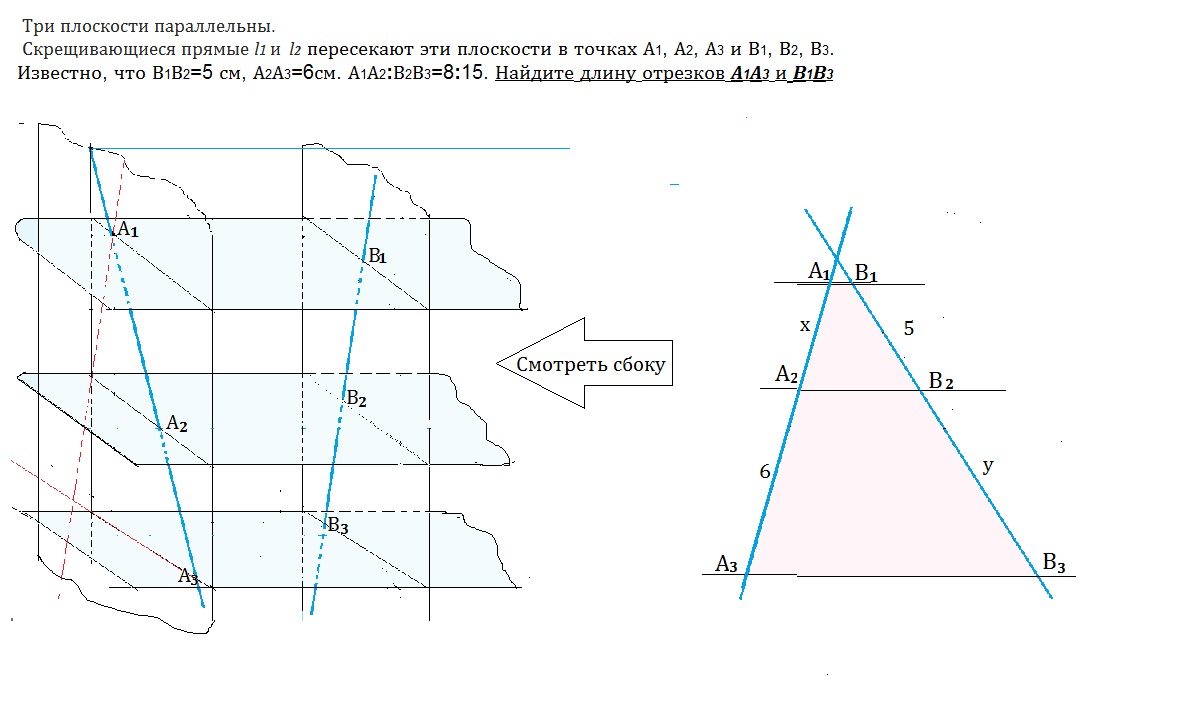
Три плоскости параллельны. Скрещивающиеся прямые l₁ и l₂ пересекают эти плоскости в точках А₁, А₂, А₃ и В₁, В₂, В₃. Известно, что В₁В₂=5 см, А₂А₃=6см. А₁А₂ : В₂В₃=8:15. Найдите длину отрезков А₁А₃ и В₁В₃
------------------
Проведем через каждую прямую плоскость. Линии пересечения плоскостей, в которых располагаются скрещивающиеся прямые, с данными 3-мя параллельными плоскостями параллельны между собой.
Сделаем рисунки.
Рис. 1 -просто для того, чтобы получить представление о расположении данных скрещивающихся прямых относительно друг друга и данных трех плоскостей. Если на эти прямые посмотреть сбоку или "перенести" параллельно одну прямую на плоскость второй прямой, то они, поскольку не параллельны друг другу по определению, как бы наложатся друг на друга и пересекутся в некоторой точке.
Тогда вид «сбоку» будет выглядеть как две прямые, пересеченные параллельными прямыми А₁В₁, А₂В₂, А₃В₃.
Рассмотрим рис. 2. - вид сбоку.
Пусть А₁А₂=х, В2В3=у
По теореме Фалеса параллельные прямые отсекают на секущих пропорциональные отрезки.
Тогда А₁А₂ : В₁В₂= х:5=6:у Из этой пропорции
ху=30
х=30/у
По условию х:у=8/15
15х=8у
х=8у:15
Приравняем найденные значения х:
30:у=8у:15
8у²=450
у²=56,25
у=7,5 см
15х=60 см
х=4 - это длина А₁А₂
Отсюда А₁А₃=4+6=10 см
В₁В₃=5+7,5=12,5 см
------------------------
Задача 11. (рисунок во втором приложении)
Параллельные плоскости альфа и бета пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла - соответственно в точках В1 и В2. Найдите АА1, если А2В2=6 см, АВ2:АВ1=3:2
Поскольку плоскости α и β параллельны, , параллельны и отрезки А1В1 и А2В2. Параллельные прямые образуют со сторонами угла подобные треугольники АА1В1 и АА2В2. Отсюда
А2В2:А1В1=АВ2:АВ1=3:2
6:А1В1=3:2
3А1В1=12 см
А1В1=4 см
Скорее всего, именно А1В1 нужно найти, т.к. АА1 найти не получится,- для этого недостаточно данных. Единственное, что можно сказать, это что по т. Фалеса АА2:АА1=3:2
* * *
Есть другое условие этой задачи:
Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла соответственно в точках В1 и В2. Найдите АА1, если А1А2=6 см. АВ2:АВ1=3:2.
По т. Фалеса АА2: АА1=АВ2:АВ1=3:2
Пусть АА1=х
Тогда АА2=х+6
Из подобия треугольников АА2 и АА1 следует отношение
(х+6):х=3:2
3х=2х+12
х=12
АА1=12 см
. Решение задачи 11 ниже.
---------------
Задача 12.
Три плоскости параллельны. Скрещивающиеся прямые l₁ и l₂ пересекают эти плоскости в точках А₁, А₂, А₃ и В₁, В₂, В₃. Известно, что В₁В₂=5 см, А₂А₃=6см. А₁А₂ : В₂В₃=8:15. Найдите длину отрезков А₁А₃ и В₁В₃
------------------
Проведем через каждую прямую плоскость. Линии пересечения плоскостей, в которых располагаются скрещивающиеся прямые, с данными 3-мя параллельными плоскостями параллельны между собой.
Сделаем рисунки.
Рис. 1 -просто для того, чтобы получить представление о расположении данных скрещивающихся прямых относительно друг друга и данных трех плоскостей. Если на эти прямые посмотреть сбоку или "перенести" параллельно одну прямую на плоскость второй прямой, то они, поскольку не параллельны друг другу по определению, как бы наложатся друг на друга и пересекутся в некоторой точке.
Тогда вид «сбоку» будет выглядеть как две прямые, пересеченные параллельными прямыми А₁В₁, А₂В₂, А₃В₃.
Рассмотрим рис. 2. - вид сбоку.
Пусть А₁А₂=х, В2В3=у
По теореме Фалеса параллельные прямые отсекают на секущих пропорциональные отрезки.
Тогда А₁А₂ : В₁В₂= х:5=6:у Из этой пропорции
ху=30
х=30/у
По условию х:у=8/15
15х=8у
х=8у:15
Приравняем найденные значения х:
30:у=8у:15
8у²=450
у²=56,25
у=7,5 см
15х=60 см
х=4 - это длина А₁А₂
Отсюда А₁А₃=4+6=10 см
В₁В₃=5+7,5=12,5 см
------------------------
Задача 11. (рисунок во втором приложении)
Параллельные плоскости альфа и бета пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла - соответственно в точках В1 и В2. Найдите АА1, если А2В2=6 см, АВ2:АВ1=3:2
Поскольку плоскости α и β параллельны, , параллельны и отрезки А1В1 и А2В2. Параллельные прямые образуют со сторонами угла подобные треугольники АА1В1 и АА2В2. Отсюда
А2В2:А1В1=АВ2:АВ1=3:2
6:А1В1=3:2
3А1В1=12 см
А1В1=4 см
Скорее всего, именно А1В1 нужно найти, т.к. АА1 найти не получится,- для этого недостаточно данных. Единственное, что можно сказать, это что по т. Фалеса АА2:АА1=3:2
* * *
Есть другое условие этой задачи:
Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла соответственно в точках В1 и В2. Найдите АА1, если А1А2=6 см. АВ2:АВ1=3:2.
По т. Фалеса АА2: АА1=АВ2:АВ1=3:2
Пусть АА1=х
Тогда АА2=х+6
Из подобия треугольников АА2 и АА1 следует отношение
(х+6):х=3:2
3х=2х+12
х=12
АА1=12 см
Приложения:

Автор ответа:
0
Ну вот, только что обратила внимание, что не ту задачу решила...
Похожие вопросы
Предмет: Қазақ тiлi,
автор: nuraylg0
Предмет: Қазақ тiлi,
автор: telmanovjannur
Предмет: Русский язык,
автор: aisulubeisenbek12
Предмет: История,
автор: olqakasibinao