Предмет: Геометрия,
автор: mamalutshaya2
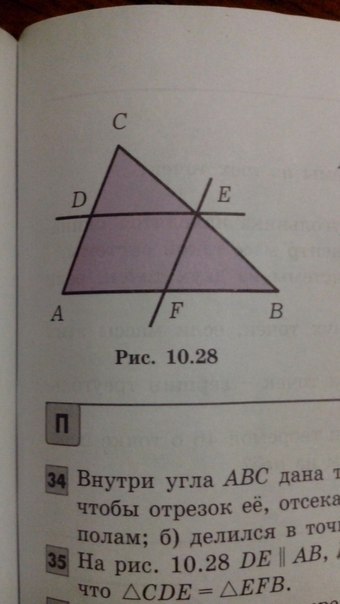
На рис. 10.28 DE ll AB; EF ll AC и D - середина отрезка АС. Докажите, что треугольник CDE = треугольнику EFB. Помогите, пожалуйста, я буду очень рада. Заранее спасибо!
Приложения:
Ответы
Автор ответа:
0
Д - середина АС, ДЕ // АВ => ДЕ - средняя линия тр.АВС
а значит Е - середина АС, а т. к. ЕФ // АС = > ЕФ - средняя линия тр. АВС
из того, что ДЕ и ЕФ - средние линии тр. АВС следую равенства:
СЕ = ЕВ
ДС = АД = ФЕ
ДЕ = АФ = ФВ
а из этих равенств следует равенство треугольников СДЕ и ЕФБ (по трем сторонам)
что и требовалось доказать
а значит Е - середина АС, а т. к. ЕФ // АС = > ЕФ - средняя линия тр. АВС
из того, что ДЕ и ЕФ - средние линии тр. АВС следую равенства:
СЕ = ЕВ
ДС = АД = ФЕ
ДЕ = АФ = ФВ
а из этих равенств следует равенство треугольников СДЕ и ЕФБ (по трем сторонам)
что и требовалось доказать
Автор ответа:
0
D - середина АС, DE|| АВ => DE - средняя линия ΔАВС⇒Е - середина BС и ЕF || АС = > ЕF - средняя линия Δ АВС⇒AF=BF
СЕ = ЕВ
DС = АD = FЕ
DЕ = ВF
Значит ΔСВУ=ΔEFB по трем сторонам/
СЕ = ЕВ
DС = АD = FЕ
DЕ = ВF
Значит ΔСВУ=ΔEFB по трем сторонам/
Похожие вопросы
Предмет: Математика,
автор: aaaavvvvvvv237
Предмет: Литература,
автор: q908
Предмет: Қазақ тiлi,
автор: okapova1990
Предмет: Обществознание,
автор: ivandianov04