Question

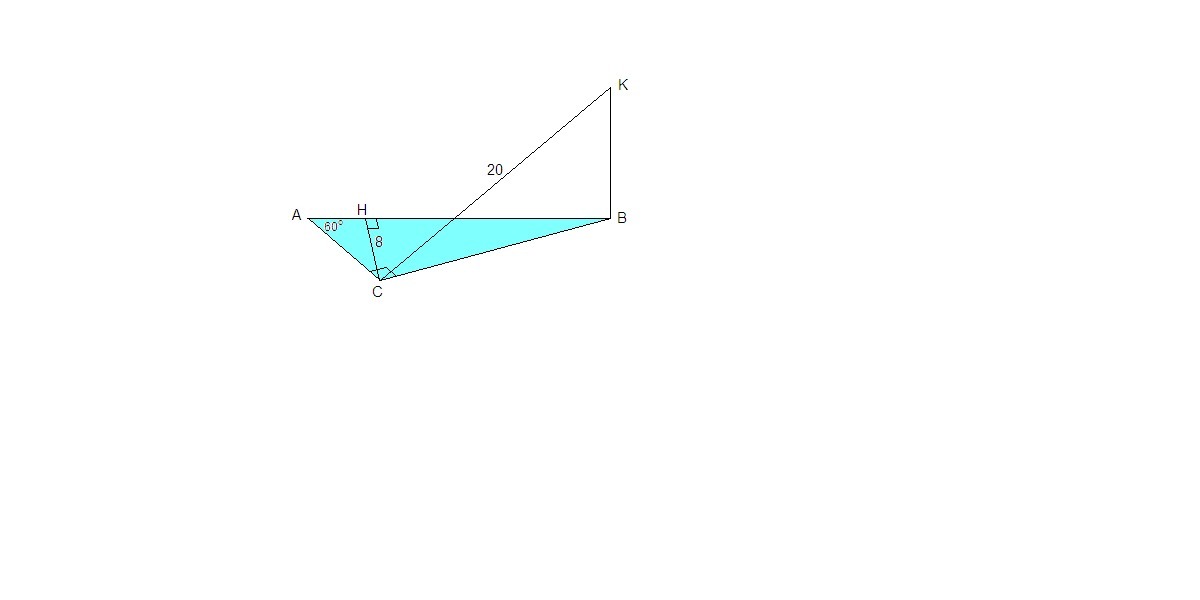
Треугольнк ABC - прямоугольный , угол A = 60 градусов , угол C = 90 градусов. CH - высота треугольника ABC , причем CH = 8 см. Отрезок BK перпендикуляр к плоскости треугольника ABC . Найдите отрезок BK , если расстояние от точки K до стороны AC равно 20 см .

Answer 1

ВС⊥АС как катеты прямоугольного треугольника,
ВС - проекция КС на плоскость треугольника, значит
КС⊥АС по теореме о трех перпендикулярах.
КС - расстояние от точки К до прямой АС,
КС = 20 см.

ΔАСН: АС = CH/sin60° = 8 / (√3/2) = 16/√3 см
ΔАВС: СВ = AC · tg60° = 16/√3 · √3 = 16 см

ΔСВК: по теореме Пифагора
             ВК = √(КС² - СВ²) = √(400 - 256) = √144 = 12 см