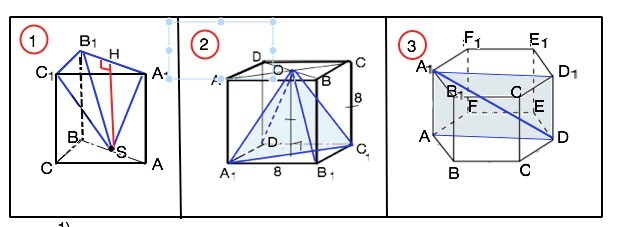
Помогите пожалуйста, хотя бы одну задачку))...они легкие для того кто хоть немного понимает геометрию...не то, что я..дуб..дубом((
№ 1
Точка S принадлежит ребру AB прямой призмы ABCA1B1C1. Длина высоты пирамиды SA1B1C1 равно длине отрезка: а)AA1 б) SA1 с) SB1
№ 2
Длина ребра куба ABCDA1B1C1D1 равна 8 дм. Точка О – точка пересечения диагоналей в основание ABCD. Вычислите площадь диагонального сечения пирамиды OA1B1C1D1
№ 3
Дина ребра шестиугольной призмы равны. Вычислите длину большей диагонали, если известно площадь боковой призмы 96 см2.
Ответы
1)
Т.к. призма прямая, её грани перпендикулярны основаниям.
Грань SA1B1 пирамиды лежит в плоскости АВВ1А1, высота SH перпендикулярна основанию А1В1С1 и параллельна боковому ребру призмы, следовательно, её длина равна длине ребра АА1.
2)
Пусть АВСD - верхнее основание куба, а нижнее A1B1C1D1.
Диагонали основания пирамиды OA1B1C1D1 совпадают с диагоналями квадрата А1В1С1D1, высота ОН равна расстоянию между параллельными основаниями куба, т.е. длине его ребер - 8 дм.
Диагональное сечение пирамиды - треугольник А1ОС1. Основание А1С1 - диагональ квадрата со стороной А1В1=8. А1С1=8√2 (как диагональ квадрата).
S(A1OC1)=OH•A1C1:2=8•8√2*2=32√2 дм²
3)
В этой задаче допущена неточность. Длины ребер правильной шестиугольной призмы равны.
В основании этой призмы правильный шестиугольник, а все 6 граней - квадраты. Площадь каждого 96:6=16 см²
Тогда ребро призмы √16=4 см.
Правильный шестиугольник можно разделить на 6 правильных треугольников, и длина бóльшей его диагонали равна длине 2-х ребер.
На рисунке приложения АD и А1D1 - бóльшие диагонали оснований, а А1D - бóльшая диагональ призмы.
По т.Пифагора
А1D=√(AA1²+AD²)=√(4²+8²)=4√5