Предмет: Алгебра,
автор: hompister
решите срочно, вроде не трудно, но я дурак
Приложения:
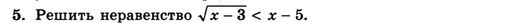
Ответы
Автор ответа:
0
Рассмотрим функцию
Область определения: подкорённое выражение должен быть неотрицательным, тоесть:
D(f) = [3;+∞)
Приравниваем функцию к нулю
Возведём обе части до квадрата
Воспользуемся свойством степеней:
Найдём дискриминант
D>0, значит уравнение имеет 2 корня
Найдём решение неравенства.
Введём на промежуток сначала область определения функции, а потом нули функции
[3]__+___(4)___+___(7)____-___>
Определение знаков:
Пусть x=8, тогда, подставив в функцию вместо х, получаем
Видим что число отрицательное, значит на промежутке (-7;+∞) будет знак МИНУС, дальше знаки меняются
Ответ:
Похожие вопросы
Предмет: История,
автор: Vladislavashamanina0
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: tanaberezovskaa133
Предмет: Химия,
автор: maxicwet
Предмет: География,
автор: atxaewa