Предмет: Геометрия,
автор: vikulichka
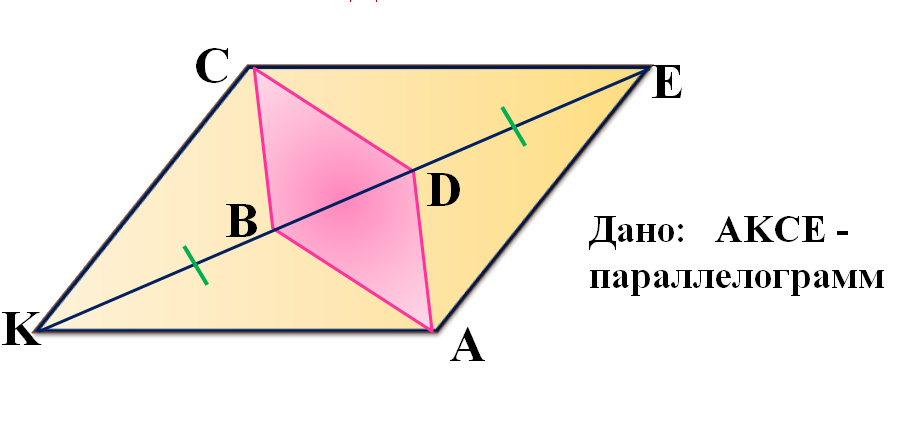
Докажите, что ABCD - параллелограмм.
Приложения:
Ответы
Автор ответа:
0
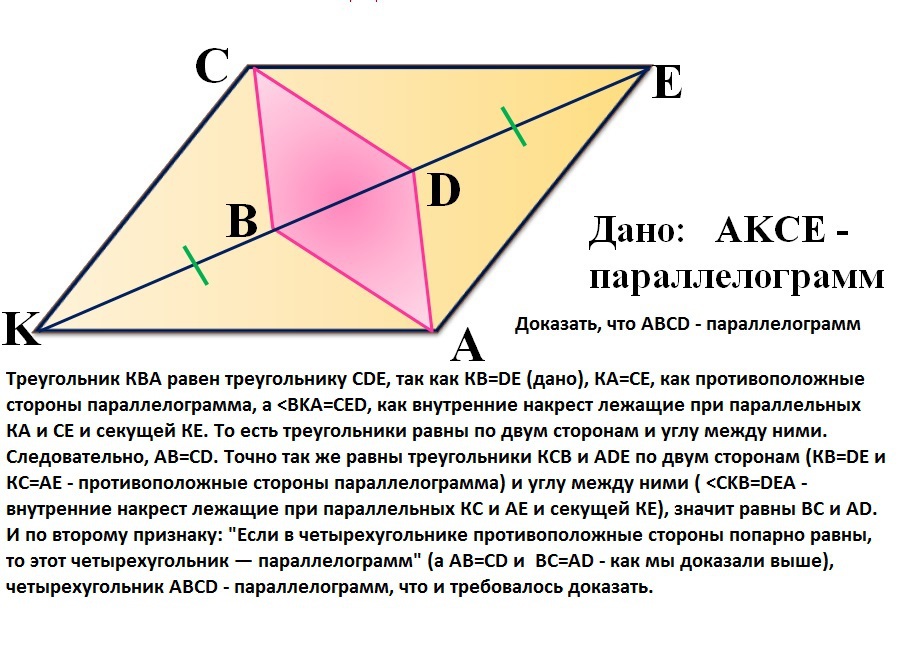
Треугольник КВА равен треугольнику СDЕ, так как КВ=DE (дано), КА=СЕ, как противоположные стороны параллелограмма, а <BKA=CED, как внутренние накрест лежащие при параллельных КА и СЕ и секущей КЕ. То есть треугольники равны по двум сторонам и углу между ними. Следовательно, АВ=CD. Точно так же равны треугольники КСВ и ADE по двум сторонам (КВ=DE и КС=АЕ - противоположные стороны параллелограмма) и углу между ними ( <CKB=DEA - внутренние накрест лежащие при параллельных КС и АЕ и секущей КЕ), значит равны ВС и AD.
И по второму признаку: "Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм" (а АВ=CD и ВС=AD - как мы доказали выше), четырехугольник АВСD - параллелограмм, что и требовалось доказать.
И по второму признаку: "Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм" (а АВ=CD и ВС=AD - как мы доказали выше), четырехугольник АВСD - параллелограмм, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Қазақ тiлi,
автор: esimovanazgul1234567
Предмет: История,
автор: sashafuglevich17
Предмет: Математика,
автор: J14
Предмет: Алгебра,
автор: DragonFlow