Пожалуйста с решением!

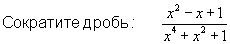
Ответы
Заметим, что
</p>
<p> </p>
<p>Первая дробь сокращается, так как числитель можно расписать по формуле разности кубов</p>
<p> </p>
<p><img src=[/tex]frac{x^3-1}{x^4+x^2+1}=frac{(x-1)*(x^2+x+1)}{x^4+x^2+1}" title="x^4+x^2+1=(x^2+x+1)*(x^2-x+1).quad (1)" title="frac{x^3-1}{x^4+x^2+1}=frac{(x-1)*(x^2+x+1)}{x^4+x^2+1}" title="x^4+x^2+1=(x^2+x+1)*(x^2-x+1).quad (1)" alt="frac{x^3-1}{x^4+x^2+1}=frac{(x-1)*(x^2+x+1)}{x^4+x^2+1}" title="x^4+x^2+1=(x^2+x+1)*(x^2-x+1).quad (1)" />
Первая дробь сокращается, так как числитель можно расписать по формуле разности кубов
Первая дробь сокращается, так как числитель можно расписать по формуле разности кубов
Сокращаем числитель и знаменатель
Заметим, что полученная дробь не сокращается. Так как корни уравнений, полученных при числителе и знаменателе будут разными. То есть из числителя получаем уравнение
х-1=0
х=1.
Если подставить х=1 в знаменатель, то получим 1, а не 0. То есть дальнейшее упрощение дроби невозможно.
Перейдем ко второй дроби. Вновь используем (1).
Как видно, эта дробь тоже несократима.