Предмет: Математика,
автор: maxtaines
Решите уравнения:
1. lim x->0 (e^-x-e^x)/sin3x)
Приложения:
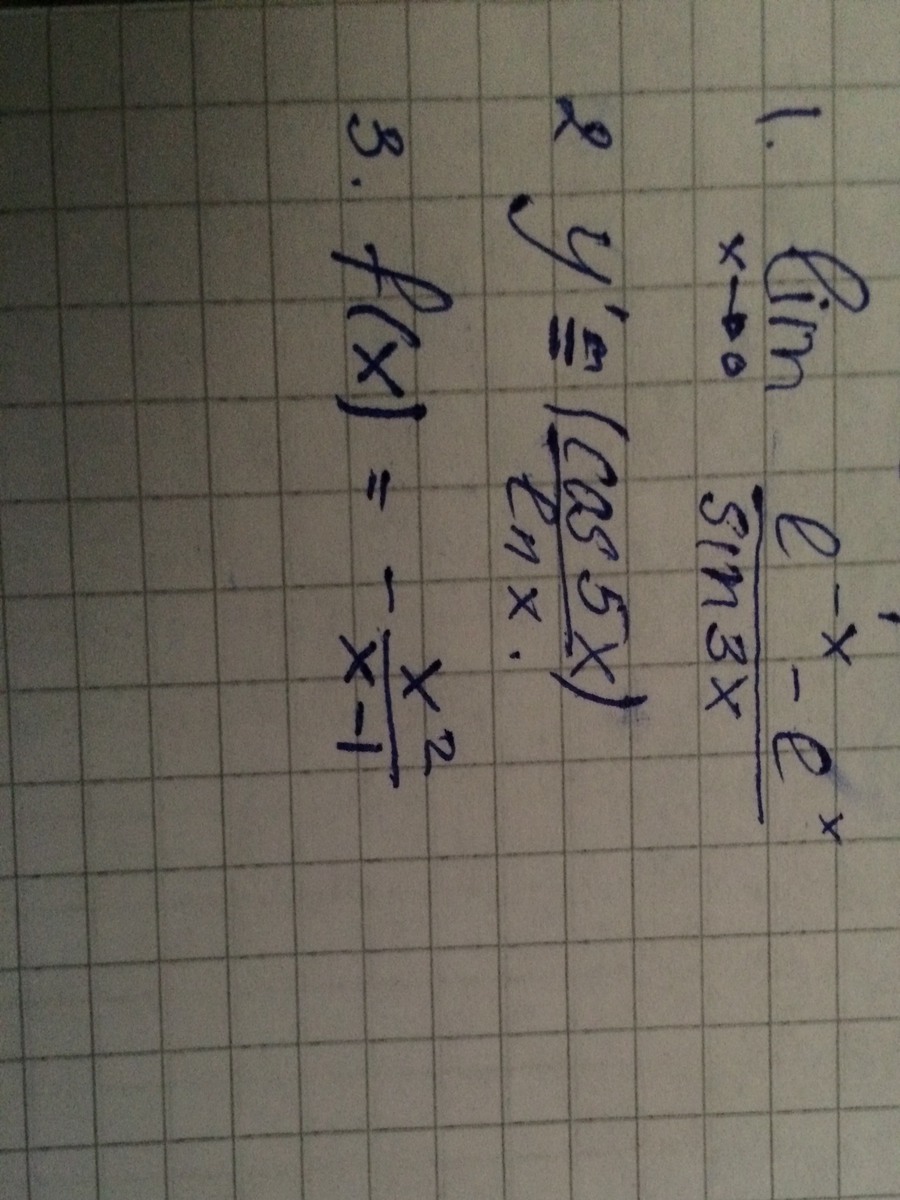
Ответы
Автор ответа:
0
Приложения:
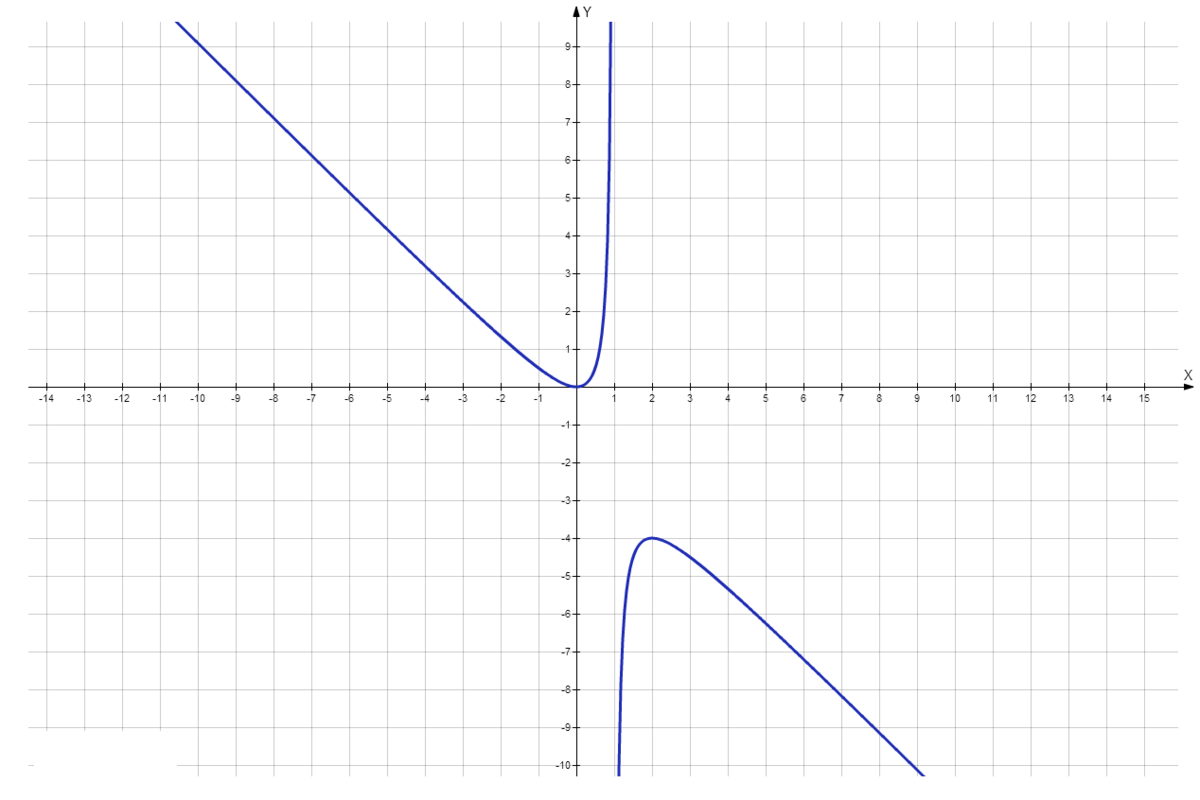
Похожие вопросы
Предмет: Английский язык,
автор: lasanovilas
Предмет: Другие предметы,
автор: gindiktsoy
Предмет: Математика,
автор: 2010Imr
Предмет: Алгебра,
автор: Anyta720