Предмет: Математика,
автор: nastya3319
помогите пожалуйста....умоляю
задания во вложении
Приложения:

Ответы
Автор ответа:
0
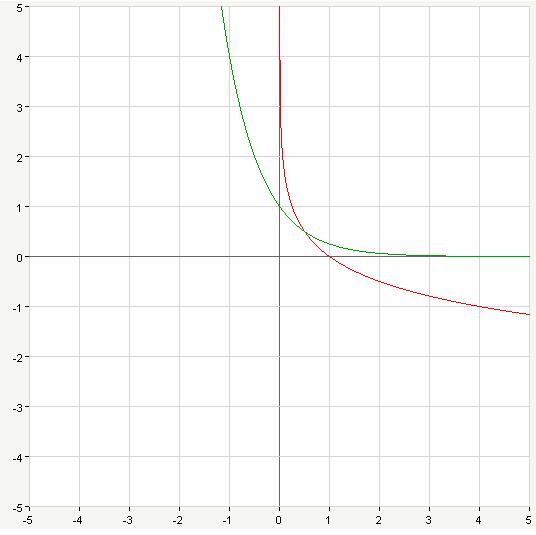
2. См. вложение - красным цветом первый график, зелёным второй.
Решение изначального неравенства сводится к решению неравенства
Приложения:
Похожие вопросы
Предмет: Математика,
автор: mila3993
Предмет: Другие предметы,
автор: polinapoctar735
Предмет: Алгебра,
автор: shahruh1237
Предмет: Физика,
автор: laden