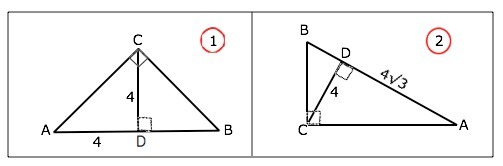
Высота CD прямоугольного треугольника ABC,проведенная из вершины прямого угла,равна 4 см.Известно,что она делит гипотенузу на отрезки,один из которых равен: 1)4 см; 2)4 умножить на корень из 3 см.Найдите градусные меры острых углов треугольника ABC.
Ответы
Найдем второй отрезок гипотенузы для каждого случая.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
a)
СD²=АD•ВD
16=4•BD
BD=16:4=4⇒
Высота СD - медиана и биссектриса ∆ АВС и делит его на два равнобедренных прямоугольных треугольника.
Острые углы такого треугольника равны 45°
б)
СD²=АD•ВD
16=4√3•BD⇒
BD=16:4√3=4/√3
Из ∆ САD:
tg∠САD=CD:AD=4:4√3=1/√3- это тангенс 30°
Из ∆ CВD:
tg∠СBD=BD:CD=(4/√3):4=√3 - это тангенс 60°
Острые углы этого треугольника 30° и 60°