Предмет: Алгебра,
автор: Дария0011
Указать посторонние корни уравнения)Помогите прошу)
Приложения:
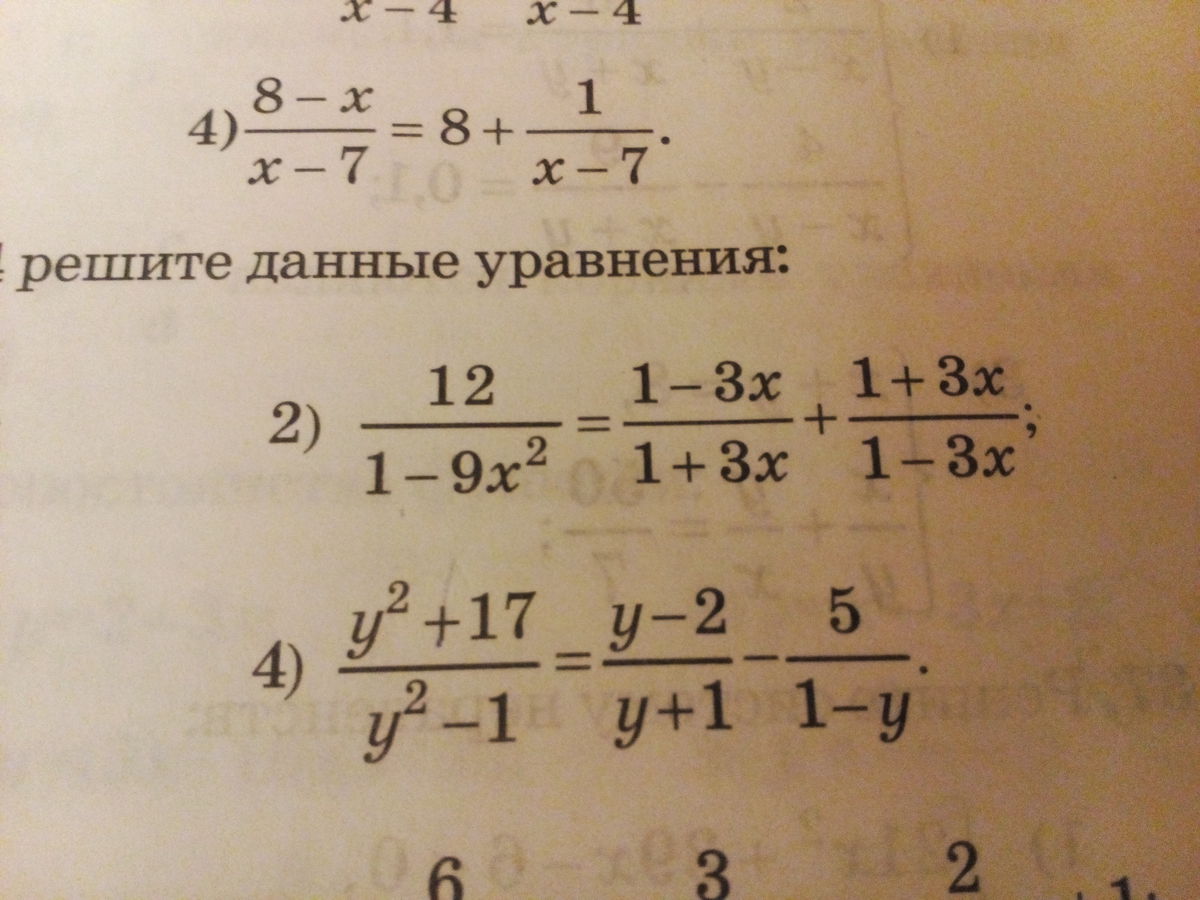
Ответы
Автор ответа:
0
2) Приводим все к общему знаменателю 1 - 9x^2 = (1-3x)(1+3x)

Переходим к числителям, которые слева и справа равны




При обоих корнях справа получается одно и тоже

А слева будет

Так что оба корня подходят, и лишних корней нет.
4) Тоже приводим к общему знам. y^2 - 1 = (y - 1)(y + 1)

Переходим к числителям, которые слева и справа равны




Проверяем
Слева будет
А слева
Тут один корень и он уж точно не лишний.
Переходим к числителям, которые слева и справа равны
При обоих корнях справа получается одно и тоже
А слева будет
Так что оба корня подходят, и лишних корней нет.
4) Тоже приводим к общему знам. y^2 - 1 = (y - 1)(y + 1)
Переходим к числителям, которые слева и справа равны
Проверяем
Слева будет
А слева
Тут один корень и он уж точно не лишний.
Похожие вопросы
Предмет: Английский язык,
автор: kakaobob
Предмет: Алгебра,
автор: v5hlghc
Предмет: Литература,
автор: WiXeRFiXeR
Предмет: Химия,
автор: scubidy
Предмет: География,
автор: NicolCarry