Предмет: Геометрия,
автор: alinaalinasam1
Прямые AB и CD параллельны, CD=BD=AD=29, BC=40. Найдите длину отрезка AC.
Ответы
Автор ответа:
0
Четырехугольник АВСD - трапеция.
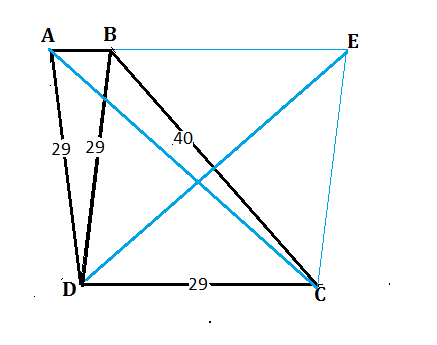
Из С проведем параллельно ВD прямую до пересечения с продолжением АВ в точке Е.
BD=СD и АВ || СD по условию, ЕС || ВD по построению, ⇒
ВЕСD - параллелограмм. ⇒
ВЕ=СD=29
СЕ=ВD=29
Четырехугольник ВЕСD - ромб.
Трапеция АDСЕ - равнобедренная (СЕ=АD).
Диагонали равнобедренной трапеции равны ⇒
АС=DЕ
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Стороны ромба равны.
ВС²+ДЕ²=4*ВD²
ВС=40
1600+DЕ²=3364
DЕ²=1764
DЕ=42
АС=DЕ=42
Из С проведем параллельно ВD прямую до пересечения с продолжением АВ в точке Е.
BD=СD и АВ || СD по условию, ЕС || ВD по построению, ⇒
ВЕСD - параллелограмм. ⇒
ВЕ=СD=29
СЕ=ВD=29
Четырехугольник ВЕСD - ромб.
Трапеция АDСЕ - равнобедренная (СЕ=АD).
Диагонали равнобедренной трапеции равны ⇒
АС=DЕ
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Стороны ромба равны.
ВС²+ДЕ²=4*ВD²
ВС=40
1600+DЕ²=3364
DЕ²=1764
DЕ=42
АС=DЕ=42
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: neredanna30
Предмет: Українська мова,
автор: alexglodorenko
Предмет: Математика,
автор: hlebokot
Предмет: Математика,
автор: tenaf83
Предмет: История,
автор: andreydukoyan