Question

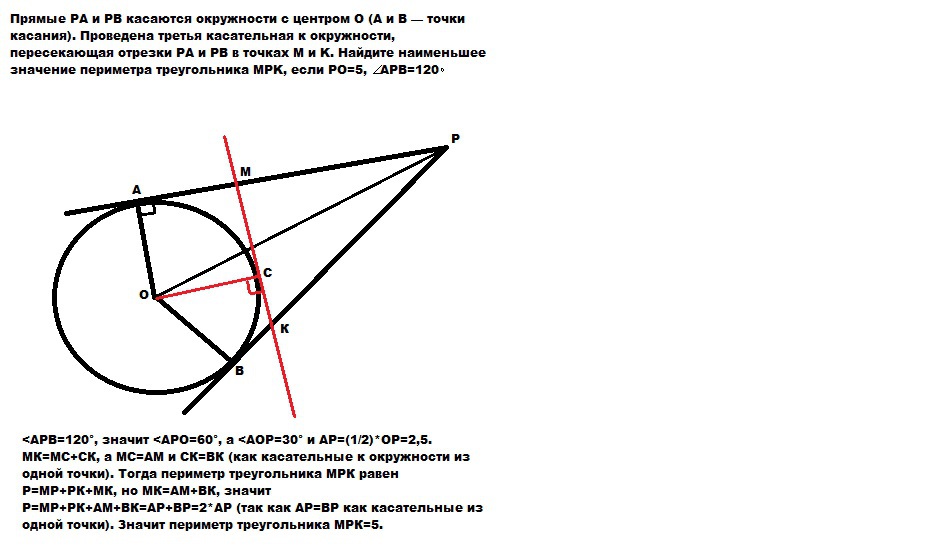
Прямые PA и PB касаются окружности с центром O (A и B — точки касания). Проведена третья касательная к окружности, пересекающая отрезки PA и PB в точках M и K. Найдите наименьшее значение периметра треугольника MPK, если PO=5, ∠APB=120∘.

Answer 1

<APB=120°, значит <APО=60°, а <AОP=30° и АР=(1/2)*ОР=2,5. (как катет, лежащий против угла 30 градусов). МК=МС+СК, а МС=АМ и СК=ВК (как касательные к окружности из одной точки). Тогда периметр треугольника МРК равен  Р=МР+РК+МК, но МК=АМ+ВК, значит Р=МР+РК+АМ+ВК=АР+ВР=2*АР (так как АР=ВР как касательные из одной точки).
Значит периметр треугольника МРК=5.