Предмет: Геометрия,
автор: diasporo
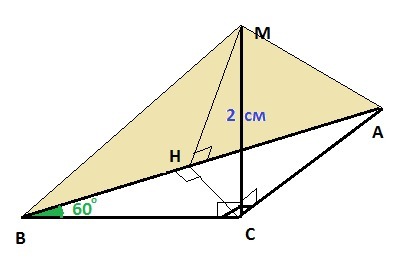
В треугольнике ABC угол C прямой, AB=2 см, угол B=60 градусов, MC перпендикулярен (ABC), MC=2 см. Найдите площадь треугольника AMB.
Напишите решение поподробнее пожалуйста
Ответы
Автор ответа:
0
ΔABC прямоугольный, ∠С = 90°, ∠B = 60°, AB = 2 см
CH ⊥ AB - высота треугольника ABC
МС ⊥ (ABC) ⇒ MC перпендикулярна любой прямой, лежащей в плоскости треугольника ABC ⇒ MC ⊥ CH
MC ⊥ CH, CH ⊥ AB ⇒ MH ⊥ AB - по теореме о трёх перпендикулярах.
ΔMCH - прямоугольный, ∠MCH = 90°, MC = 2 см, см. По теореме Пифагора
Ответ: 0,5√19 см²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: 23060900
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: ekaterinabikbulatova
Предмет: Алгебра,
автор: Roym
Предмет: Математика,
автор: НаФ