Предмет: Алгебра,
автор: walley8
Найдите корни уравнений 2sinx-cosx=1-sin2x,принадлежащие полуинтервалу
[-p;5p/6)
Ответы
Автор ответа:
0
1)
2)
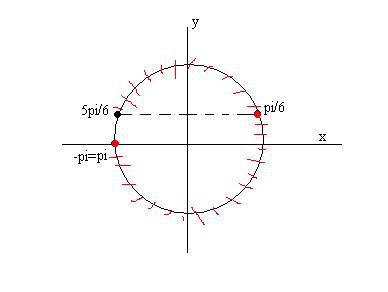
Выборка корней (см. рисунок): красным заштрихован интервал, данный в условии задачи. Красными точками отмечены корни, попавшие в указанный интервал, черная точка - не попала в интервал.
Ответ:
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: 7002lVetErOKl2007
Предмет: Биология,
автор: kraftnz
Предмет: История,
автор: Аноним
Предмет: Литература,
автор: 111yana01