Предмет: Алгебра,
автор: aniyn
Решите,пожалуйста
Решить системы уравнений
Картинка прилагается
Приложения:
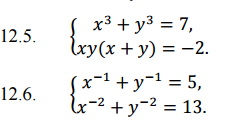
Ответы
Автор ответа:
0
12.5.



Складываем уравнения





Получаем теорему Виета

Это значит, что x и y являются корнями уравнения

t1=-1; t2 = 2
Ответ: (-1; 2); (2; -1)
12.6.

Замена x^(-1) = 1/x = m; y^(-1) = 1/y = n



Подставляем 1 уравнение во 2 уравнение

Получаем теорему Виета

Это значит, что m и n являются корнями уравнения

m1 = 1/x = 2; x1 = 1/2; n1 = 1/y = 3; y1 = 1/3
m2 = 1/x = 3; x1 = 1/3; n2 = 1/y = 2; y2 = 1/2
Ответ: (1/2; 1/3); (1/3; 1/2)
Складываем уравнения
Получаем теорему Виета
Это значит, что x и y являются корнями уравнения
t1=-1; t2 = 2
Ответ: (-1; 2); (2; -1)
12.6.
Замена x^(-1) = 1/x = m; y^(-1) = 1/y = n
Подставляем 1 уравнение во 2 уравнение
Получаем теорему Виета
Это значит, что m и n являются корнями уравнения
m1 = 1/x = 2; x1 = 1/2; n1 = 1/y = 3; y1 = 1/3
m2 = 1/x = 3; x1 = 1/3; n2 = 1/y = 2; y2 = 1/2
Ответ: (1/2; 1/3); (1/3; 1/2)
Автор ответа:
0
Спасибо! Проверите решение у этих номеров потом? Я вам доверяю ♥
http://znanija.com/task/12668291
http://znanija.com/task/12668292
http://znanija.com/task/12668291
http://znanija.com/task/12668292
Автор ответа:
0
91 - правильно
Автор ответа:
0
92 тоже вроде правильно, но номер 12.10 какой-то уж очень неуклюжий получился. Нет ли там ошибки в задании?
Автор ответа:
0
В задании нет. Я вот насчет него и не уверенна была
Автор ответа:
0
номер 12.10 верно))более красиво можно было бы записать ответ x=2^(3/5)/13^(2/5) y=13^(3/5)/2^(2/5)
Похожие вопросы
Предмет: Алгебра,
автор: micha57
Предмет: Математика,
автор: warship32
Предмет: Английский язык,
автор: lleonovich707
Предмет: География,
автор: Санёёёк
Предмет: Математика,
автор: НадёнаБахарева