Предмет: Алгебра,
автор: Julia34region
Помогите решить неравенство))
Приложения:
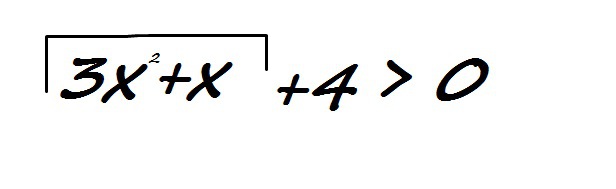
Ответы
Автор ответа:
0
так как √(3х²+х)≥0, то √(3х²+х) +4>0 всегда >0 при любом допустимом х.
ОДЗ:
3х²+х≥0
3х²+х=0
х(3х+1)=0
х=0
3х+1=0 ; х=-1/3
+ - +
----------*---------*---------->
-1/3 0
отв:х∈(-бесконечность; -1/3] U [0;+бесконечность)
ОДЗ:
3х²+х≥0
3х²+х=0
х(3х+1)=0
х=0
3х+1=0 ; х=-1/3
+ - +
----------*---------*---------->
-1/3 0
отв:х∈(-бесконечность; -1/3] U [0;+бесконечность)
Автор ответа:
0
а 4 куда потеряла?
Автор ответа:
0
что?
Автор ответа:
0
ответ правильный,спасибо))
Автор ответа:
0
3x^2 + x - находится под квадратным корнем?
Если да, то это арифметический корень, он неотрицателен, и поэтому левая часть положительна при любом х, входящем в область определения.
Область определения:
3x^2 + x >= 0
x(3x + 1) >= 0
x = (-oo; -1/3] U [0; +oo)
А если не под квадратным корнем, тогда решаем квадратное неравенство
3x^2 + x + 4 > 0
D = 1 - 4*3*4 < 0
Это неравенство верно при любом x.
x = (-oo; +oo)
Если да, то это арифметический корень, он неотрицателен, и поэтому левая часть положительна при любом х, входящем в область определения.
Область определения:
3x^2 + x >= 0
x(3x + 1) >= 0
x = (-oo; -1/3] U [0; +oo)
А если не под квадратным корнем, тогда решаем квадратное неравенство
3x^2 + x + 4 > 0
D = 1 - 4*3*4 < 0
Это неравенство верно при любом x.
x = (-oo; +oo)
Похожие вопросы
Предмет: Русский язык,
автор: nazarenkodanil627
Предмет: Информатика,
автор: hodzhabekova8395
Предмет: Литература,
автор: aroslavpronin92006
Предмет: История,
автор: Аноним
Предмет: Химия,
автор: Lubsia