Предмет: Алгебра,
автор: denchikosipov
Вот, не могу никак прийти к решению. Вроде не так уж прям и сложно должно быть всё ведь.
Приложения:
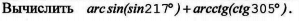
Kulakca:
алгоритмов нет и быть не может к таким задачам
вообще говоря, задача не очень и простая
сейчас постараюсь пояснить основные идеи решения
Ответы
Автор ответа:
0
Если мне окончательно не отшибло память, то arcsin(sin(x))=x, при -pi/2<x<pi/2. Так же и для arcctg(ctg(x))=x при 0<x<pi.
получим arcsin(-sin(37))=-37гр.
По свойству arcctg(-x)=pi-arcctg(x) получим ctg(305)=-ctg(55), тогда arcctg(-ctg(55))=180- arcctg(ctg(55))=125 гр.
Итого -37+125=88 гр.
ну это вы уж загнули ;)
наоборот надо было
sin(arcsin x) = x
здесь идея другая. Обозначьте arcsin(din 217) за a
дальше используем определение арксинуса.
не, здесь все неверно...
это формула верна только для x от -pi/2 до pi/2
Автор ответа:
1
sin 217° = - sin 37° => arcsin(-sin 37°) = -37°
ctg 305° = - ctg 55° => arcctg(-ctg 55°) = 180° - arcctg(ctg 55°) = 180° - 55° = 125°
=> -37° + 125° = 88°
Ответ: 88°.
ctg 305° = - ctg 55° => arcctg(-ctg 55°) = 180° - arcctg(ctg 55°) = 180° - 55° = 125°
=> -37° + 125° = 88°
Ответ: 88°.
Решение верное, ибо совпадает с ответом. Но как осуществляется этот перевод, что sin 217° = - sin 37° и такой же с катангенсом?
формулы приведения, мистер)))
Ох, точно, забыл весь школьный курс уже) Мерси!
на здоровье! ))
Похожие вопросы
Предмет: Русский язык,
автор: 2008бобо
Предмет: Другие предметы,
автор: renatnabiev2011
Предмет: Английский язык,
автор: sysoeyaVika
Предмет: Математика,
автор: Sasok630
Предмет: Алгебра,
автор: mirzounarbayzozoda