Question

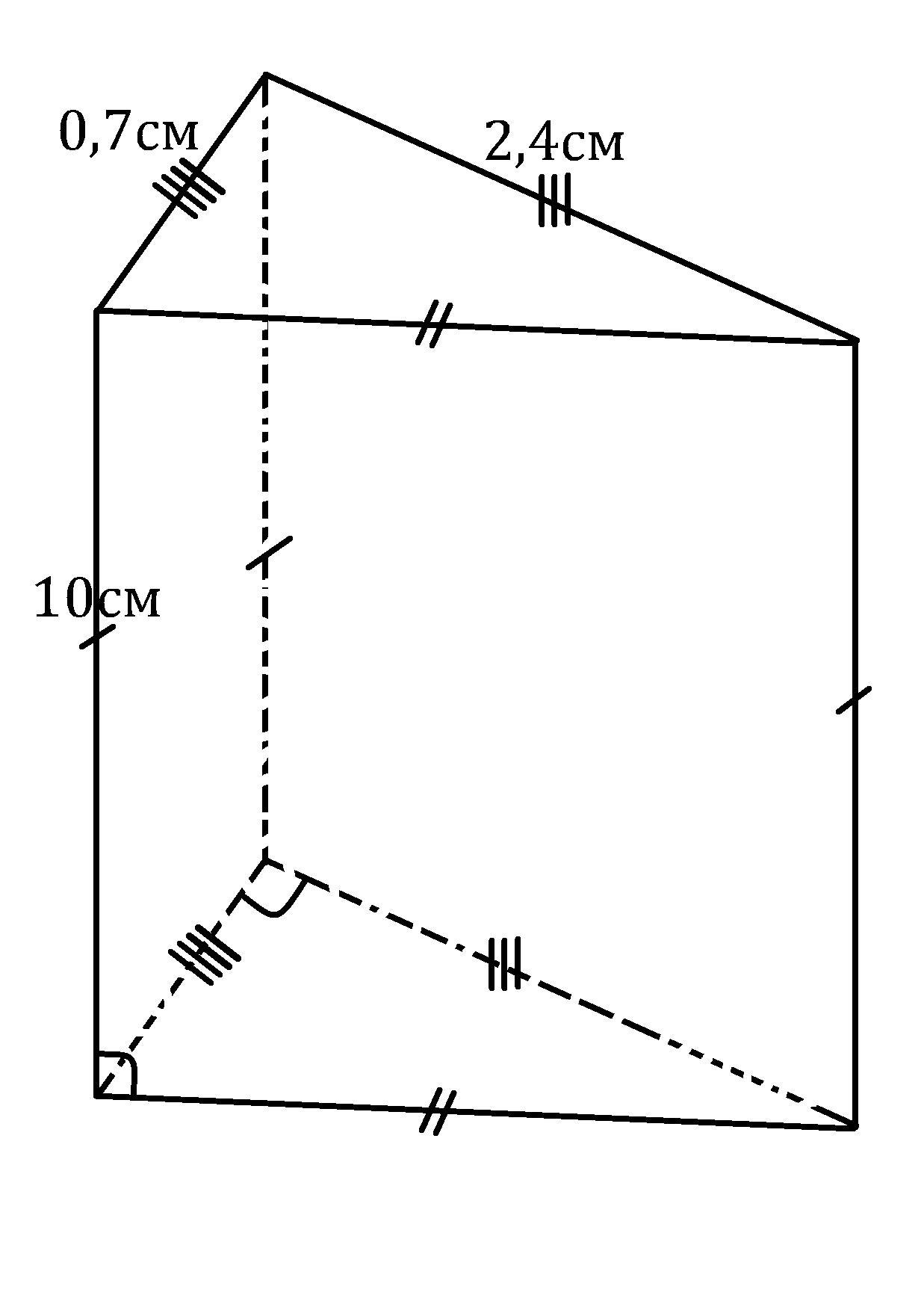
Основание прямой треугольной призмы является прямоугольный треугольник с катетами 0.7 см и 2.4 см , боковое ребро призмы ровно 10 см. Найдите площади боковой и полной поверхности призмы.

Answer 1

В прямой призме боковые грани это прямоугольники.

Найдём по теореме Пифагора гипотенузу прямоугольного треугольника из оснований.

$\displaystyle \sqrt{0,\! 7^2 +2,\! 4^2 } =\frac{\sqrt{7^2 +24^2 } }{10}=\frac{\sqrt{25^2 }}{10} =2,\! 5$ см

Площадь боковой поверхности найдём как сумму площадей прямоугольников:

S(бок.) = 10·0,7 + 10·2,4 + 10·2,5 = 10·(0,7+2,4+2,5) = 10·5,6 = 56 см².

Площадь одного основания найдём как площадь прямоугольного треугольника, через катеты:

$\displaystyle \frac12 \cdot 0,\! 7\cdot 2,\! 4=1,\! 68:2=0,\! 84$ см²

Тогда S(осн.) = 0,84·2 = 1,68 см².

S(пол.) = S(бок.) + S(осн.) = 56+1,68 = 57,68 см².

Ответ: 1,68 см² - площадь боковой поверхности; 57,68 см² - площадь полной поверхности.