Предмет: Алгебра,
автор: intoxi
Помогите решить, пожалуйста!
Приложения:
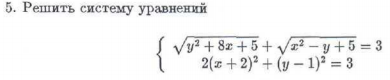
Ответы
Автор ответа:
1
Пришлось повозиться
{ √(y^2 + 8x + 5) + √(x^2 - y + 5) = 3
{ 2(x + 2)^2 + (y - 1)^2 = 3
Второе уравнение
2(x^2 + 4x + 4) + (y^2 - 2y + 1) = 3
2x^2 + 8x + 8 + y^2 - 2y + 1 - 3 = 0
2x^2 + 8x + y^2 - 2y + 6 = 0
2(x^2 - y + 5) + (y^2 + 8x + 5) - 9 = 0
Замена (y^2 + 8x + 5) = a; (x^2 - y + 5) = b
{ √a + √b = 3
{ 2b + a - 9 = 0
Подстановка
{ a = 9 - 2b
{ √(9 - 2b) = 3 - √b
Возводим в квадрат 2 уравнение
9 - 2b = 9 - 6√b + b
6√b = 3b
2√b = b
4b = b^2
b1 = 0; a1 = 9
b2 = 4; a2 = 1
Обратная замена. Получаем две системы
1)
{ y^2 + 8x + 5 = 9
{ x^2 - y + 5 = 0
Подстановка
{ y = x^2 + 5
{ (x^2 + 5)^2 + 8x - 4 = 0
x^4 + 10x^2 + 25 + 8x - 4 = 0
x^4 + 10x^2 + 8x + 21 = 0
Рассмотрим это уравнение как функцию и найдем ее минимум.
F(x) = x^4 + 10x^2 + 8x + 21 = 0
F'(x) = 4x^3 + 20x + 8 = 4(x^3 + 5x + 2) = 0
F'(-1) = 4(-1 - 5 + 2) = 4*(-4) = -16 < 0
F'(0) = 4*2 = 8 > 0
Очевидно, что корень уравнения F'(x) = 0
иррациональный и принадлежит -1 < x0 < 0
Уточним корень с точностью 0,1
F'(-0,4) = F'(-2/5) = 4(-8/125 - 2 + 2) = -32/125 < 0
F'(-0,3) = F'(-3/10) = 4(-27/1000 - 3/2 + 2) = 4(1/2 - 27/1000) > 0
Уточнили, -0,4 < x0 < -0,3
Найдем значения F(x) в этих точках
F(-0,4) = (-0,4)^4 + 10(-0,4)^2 - 8*0,4 + 21 = 19,4256
F(-0,3) = (-0,3)^4 + 10(-0,3)^2 - 8*0,3 + 21 = 19,5081
Оба значения намного больше 0, значит и в точке x0
значение минимума F(x0) > 0.
То есть график нигде не пересекает ось Ох.
Это уравнение действительных корней не имеет.
2)
{ y^2 + 8x + 5 = 1
{ x^2 - y + 5 = 4
Подстановка
{ y = x^2 + 1
{ (x^2 + 1)^2 + 8x + 4 = 0
x^4 + 2x^2 + 1 + 8x + 4 = 0
x^4 + 2x^2 + 8x + 5 = 0
x^4 + x^3 - x^3 - x^2 + 3x^2 + 3x + 5x + 5 = 0
(x + 1)(x^3 - x^2 + 3x + 5) = 0
(x + 1)(x^3 + x^2 - 2x^2 - 2x + 5x + 5) = 0
(x + 1)(x + 1)(x^2 - 2x + 5) = 0
x1 = x2 = -1, третья скобка корней не имеет.
y1 = y2 = x^2 + 1 = 1 + 1 = 2
Ответ: (-1; 2)
{ √(y^2 + 8x + 5) + √(x^2 - y + 5) = 3
{ 2(x + 2)^2 + (y - 1)^2 = 3
Второе уравнение
2(x^2 + 4x + 4) + (y^2 - 2y + 1) = 3
2x^2 + 8x + 8 + y^2 - 2y + 1 - 3 = 0
2x^2 + 8x + y^2 - 2y + 6 = 0
2(x^2 - y + 5) + (y^2 + 8x + 5) - 9 = 0
Замена (y^2 + 8x + 5) = a; (x^2 - y + 5) = b
{ √a + √b = 3
{ 2b + a - 9 = 0
Подстановка
{ a = 9 - 2b
{ √(9 - 2b) = 3 - √b
Возводим в квадрат 2 уравнение
9 - 2b = 9 - 6√b + b
6√b = 3b
2√b = b
4b = b^2
b1 = 0; a1 = 9
b2 = 4; a2 = 1
Обратная замена. Получаем две системы
1)
{ y^2 + 8x + 5 = 9
{ x^2 - y + 5 = 0
Подстановка
{ y = x^2 + 5
{ (x^2 + 5)^2 + 8x - 4 = 0
x^4 + 10x^2 + 25 + 8x - 4 = 0
x^4 + 10x^2 + 8x + 21 = 0
Рассмотрим это уравнение как функцию и найдем ее минимум.
F(x) = x^4 + 10x^2 + 8x + 21 = 0
F'(x) = 4x^3 + 20x + 8 = 4(x^3 + 5x + 2) = 0
F'(-1) = 4(-1 - 5 + 2) = 4*(-4) = -16 < 0
F'(0) = 4*2 = 8 > 0
Очевидно, что корень уравнения F'(x) = 0
иррациональный и принадлежит -1 < x0 < 0
Уточним корень с точностью 0,1
F'(-0,4) = F'(-2/5) = 4(-8/125 - 2 + 2) = -32/125 < 0
F'(-0,3) = F'(-3/10) = 4(-27/1000 - 3/2 + 2) = 4(1/2 - 27/1000) > 0
Уточнили, -0,4 < x0 < -0,3
Найдем значения F(x) в этих точках
F(-0,4) = (-0,4)^4 + 10(-0,4)^2 - 8*0,4 + 21 = 19,4256
F(-0,3) = (-0,3)^4 + 10(-0,3)^2 - 8*0,3 + 21 = 19,5081
Оба значения намного больше 0, значит и в точке x0
значение минимума F(x0) > 0.
То есть график нигде не пересекает ось Ох.
Это уравнение действительных корней не имеет.
2)
{ y^2 + 8x + 5 = 1
{ x^2 - y + 5 = 4
Подстановка
{ y = x^2 + 1
{ (x^2 + 1)^2 + 8x + 4 = 0
x^4 + 2x^2 + 1 + 8x + 4 = 0
x^4 + 2x^2 + 8x + 5 = 0
x^4 + x^3 - x^3 - x^2 + 3x^2 + 3x + 5x + 5 = 0
(x + 1)(x^3 - x^2 + 3x + 5) = 0
(x + 1)(x^3 + x^2 - 2x^2 - 2x + 5x + 5) = 0
(x + 1)(x + 1)(x^2 - 2x + 5) = 0
x1 = x2 = -1, третья скобка корней не имеет.
y1 = y2 = x^2 + 1 = 1 + 1 = 2
Ответ: (-1; 2)
Похожие вопросы
Предмет: Русский язык,
автор: айя36
Предмет: Русский язык,
автор: nanaku1
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: dresti
Предмет: Русский язык,
автор: svetlana61k46