Предмет: Геометрия,
автор: Temach282
Помогите решить
В треугольнике MBO построена высота BH. Известно, что BO=5, OH=4, а радиус окружности около треугольника MBO, равен 10. Найдите длину стороны MB.
решение пишите полностью(знаю что пифагора)
Ответы
Автор ответа:
7
Дано:
MBO - треугольник
BH - высота
BO = 5
OH = 4
Найти:
MB - ?
Решение:
Рассмотрим треугольник BHO; в нем BO = 5, OH = 4 ( по условию ); BH = BO² - OH² = 5² - 4² = 25 - 16 = 9² = 3; следовательно, треугольник BHO - египетский (стороны 3,4,5). Найдем длину сторон MB по теореме синусов. Пусть MB = x. Находим x по формуле 2R*sin (sin см. на фото во вложении ∠O). Исходя из того что треугольник BHO - египетский, находим sin = . х = 2 * 10 *
. х = 2 * 10 *  = 12. MB = 12
= 12. MB = 12
MBO - треугольник
BH - высота
BO = 5
OH = 4
Найти:
MB - ?
Решение:
Рассмотрим треугольник BHO; в нем BO = 5, OH = 4 ( по условию ); BH = BO² - OH² = 5² - 4² = 25 - 16 = 9² = 3; следовательно, треугольник BHO - египетский (стороны 3,4,5). Найдем длину сторон MB по теореме синусов. Пусть MB = x. Находим x по формуле 2R*sin (sin см. на фото во вложении ∠O). Исходя из того что треугольник BHO - египетский, находим sin =
Приложения:
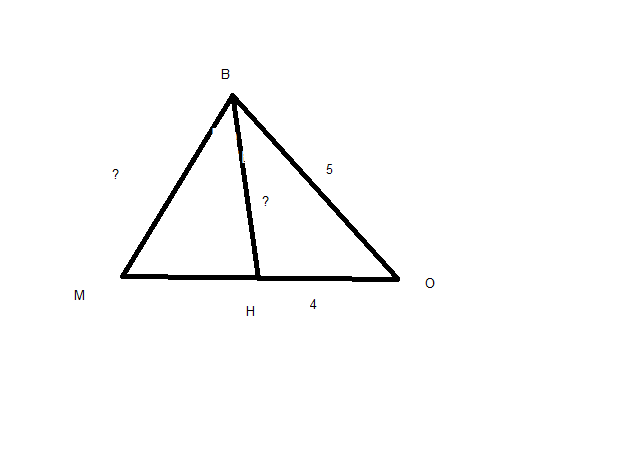
Похожие вопросы
Предмет: Другие предметы,
автор: умница646
Предмет: Русский язык,
автор: bars19
Предмет: Русский язык,
автор: Umed7770
Предмет: Английский язык,
автор: WhatHappened
Предмет: Қазақ тiлi,
автор: Behruza1908