Предмет: Геометрия,
автор: alyaalechka
Катеты прямоугольного треугольника равны 6 см и 8 см . Найти длину высоты, опущенной на гипотенузу.
Если можно я решением
Ответы
Автор ответа:
19
Прямоугольный треугольник, в котором отношение катетов равно 3:4 ( как здесь) - египетский. Гипотенуза равна 10 см ( можно проверить т.Пифагора).
Высота прямоугольного треугольника из прямого угла к гипотенузе - есть среднее геометрическое (среднее пропорциональное) двух образованных ею отрезков гипотенузы.
Пусть треугольник будет АВС, высота СН, отрезок ВН равен х, отрезок АН= 10-х
СН²=ВН*(АВ-ВН)=х*(10-х)
В то же время
катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу.
Возьмем катет ВС=6:
6²=10*х
Тогда х=3,6 см.
h²=3,6*(10-3,6)=23,04
h=4,8 см------
Т.к. высота прямоугольного треугольника из вершины прямого угла к гипотенузе делит его на два подобных, можно задачу решать через подобие.
Высота прямоугольного треугольника из прямого угла к гипотенузе - есть среднее геометрическое (среднее пропорциональное) двух образованных ею отрезков гипотенузы.
Пусть треугольник будет АВС, высота СН, отрезок ВН равен х, отрезок АН= 10-х
СН²=ВН*(АВ-ВН)=х*(10-х)
В то же время
катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу.
Возьмем катет ВС=6:
6²=10*х
Тогда х=3,6 см.
h²=3,6*(10-3,6)=23,04
h=4,8 см------
Т.к. высота прямоугольного треугольника из вершины прямого угла к гипотенузе делит его на два подобных, можно задачу решать через подобие.
Приложения:
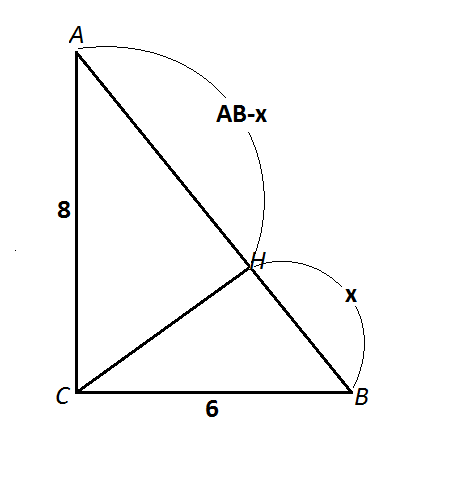
Похожие вопросы
Предмет: Русский язык,
автор: tanyafox1
Предмет: Русский язык,
автор: danjiw4
Предмет: Русский язык,
автор: айым62
Предмет: История,
автор: 20020227